Nearest Distance Calculation Based on GJK Algorithm

Date: July 25, 2014

Basic Algorithm Principles

Estimating the Nearest Distance Using the GJK Algorithm

The GJK (Gilbert-Johnson-Keerthi) algorithm is a collision detection algorithm. Using the GJK algorithm to calculate the shortest distance between two convex polygons is essentially finding the distance from their Minkowski difference to the origin. If the Minkowski difference contains the origin, it indicates that the two convex polygons intersect.

The Minkowski difference is conceptually similar to the Minkowski sum.

Assume there are two objects. The Minkowski sum of these objects is the set of all sums of points from object A and points from object B, i.e.,

\[A+B=\{a+b|a\in A,b\in B\}\]

It is clear that if both objects are convex, their Minkowski sum is also convex. The Minkowski difference is the concept of the Minkowski sum with respect to subtraction and can be represented as:

\[A-B=\{a-b|a\in A,b\in B\}\]

If the two convex polygons do not collide, their Minkowski difference does not contain the origin. In this case, the shortest distance between them is the nearest distance from the shape of their Minkowski difference to the origin.

Accelerating Searches with Kd_tree

Kd_tree (K-dimensional tree) is a data structure used for partitioning data points in a k-dimensional space. A Kd_tree is a binary tree where each node represents a spatial range. It facilitates fast matching by creating data indexes, as real-world data often clusters together. By designing effective indexing structures, the search speed can be significantly improved.

In C++, the ANN (A Library for Approximate Nearest Neighbor Searching) library can be used to implement Kd_tree-related algorithms. ANN is a C++ library that supports various data structures and algorithms for high-dimensional nearest neighbor searches.

KNN Algorithm

The KNN (k-Nearest Neighbor) classification algorithm is one of the simplest machine learning algorithms. The idea is that if a sample belongs to the same category as the majority of its k nearest neighbors in the feature space, then the sample is also classified into that category. In the KNN algorithm, the selected neighboring samples are correctly classified objects.

KNN can be used for both classification and regression. By finding the k nearest neighbors of a sample and assigning the average attribute value of these neighbors to the sample, the sample’s attributes can be determined.

A major drawback of the KNN algorithm is when the samples are imbalanced. If the sample size of one class is much larger than others, a new sample’s k nearest neighbors might be dominated by this large class, leading to biased classification.

CUDA Principles

CUDA (Compute Unified Device Architecture) is a computing platform introduced by NVIDIA, allowing GPUs to handle complex computational problems. Developers can write programs for the CUDA architecture using the C language.

Using a GPU for computation offers several advantages over using a CPU:

GPUs generally have higher memory bandwidth. For example, the NVIDIA GeForce 8800GTX has a memory bandwidth exceeding 50GB/s, while high-end CPUs have memory bandwidths around 10GB/s.
GPUs have a larger number of execution units. For instance, the GeForce 8800GTX has 128 “stream processors” running at 1.35GHz. Although CPUs typically have higher frequencies, they have far fewer execution units.
Compared to high-end CPUs, GPUs are relatively inexpensive. For example, a GeForce 8800GT with 512MB of memory costs about the same as a 2.4GHz quad-core CPU.

CUDA code is divided into two parts: one part runs on the host (CPU) and is standard C code, while the other part runs on the device (GPU) and is parallel code, called a kernel, compiled by nvcc. All threads generated by the kernel form a Grid. After the parallel section ends, the program returns to the serial part and runs on the host.

In CUDA, the host and device have separate memory spaces. Therefore, when executing a kernel on the device, the programmer needs to transfer data from host memory to allocated device memory. After the device completes its execution, the results need to be transferred back to the host, and the device memory should be freed. The CUDA runtime system provides an API for programmers to perform these tasks.

Algorithm Implementation Process

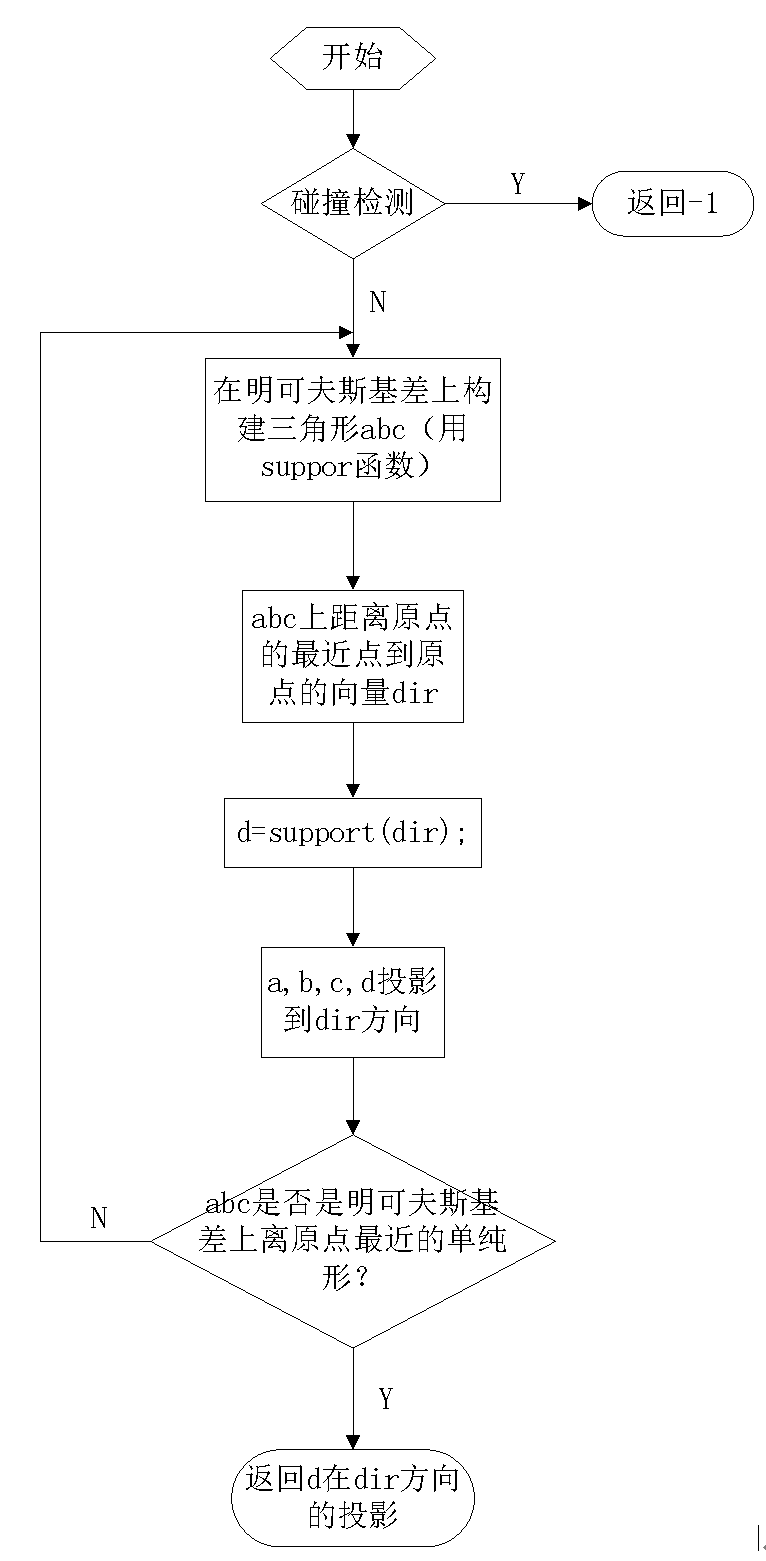
Implementing the GJK Algorithm

The process is shown in the diagram below.

GJK

Implementing Kd_tree with ANN

Assume there are objects A and B. For object B, allocate a memory space to store all points in B and define a pointer of the ANNpointArray class to point to this memory space. Build a Kd_tree structure using the points from object B, and store it in the ANNkd_tree class. For each point in object A, assign it to the ANNpoint class as a query point. Use the annkSearch function in the ANNkd_tree class to search for points in object B and find the nearest neighbor as the closest point to a given point in object A.

Once the nearest point is found, calculate the distance directly using the Euclidean distance formula. Then, compare the distances corresponding to each point in object A to determine the closest point between objects A and B.

Implementing Point-to-Face Distance

For sparsely sampled objects, the closest points obtained using the Kd_tree algorithm may differ significantly from the actual closest points between the two objects. However, for objects with relatively uniform surfaces, dense sampling can be inefficient and uninformative. In such cases, using point-to-face distance to determine the nearest point outside a triangle is proposed.

Implementation method:

Assume objects A and B. Use the Kd_tree algorithm to find the nearest points a and b. Identify the triangle on object B where point b lies (there may be more than one). For each triangle, find the point closest to a, and through successive comparisons, determine the point corresponding to the shortest distance as the nearest point between the two objects.

As shown in the diagram below, the teapot is object A, and the cylinder is object B, with sampling points only on the top and bottom circumferences of object B.

Algorithm Testing

GJK

Implementation speed: ~90 fps (sampling points of 10,000 and 2,500 for the two objects, respectively).

Collision detection performance is quite stable.

Distance calculation is also fairly accurate.

Issues:

Determining the nearest point: The GJK algorithm itself does not involve determining the nearest point. It achieves high speed by avoiding point traversal through iterative algorithms. Therefore, it cannot determine the nearest point intrinsically and requires other methods to do so.
The GJK algorithm is only suitable for convex polygons or convex polyhedra. In practical applications, it may not be directly usable for most cases, which raises the issue of how to decompose complex objects into multiple convex polyhedra. The decomposition process must meet real-time and accuracy requirements.

ANN

Implementation speed: ~30 fps (sampling points of 5,000 for each object).

The nearest point search results are quite stable. Since it only involves searching for points, it has strong adaptability and no special requirements for the shape of the objects.