Semantic Line Segment Fitting and Registration Scheme for AVP Applications
Date:
Semantic Line Segment Fitting
Communication Record
- Line segment extraction method based on random sampling and region growing;
- Use PCA algorithm to determine the center point and direction of each line segment, and then calculate the endpoints of the line segments;
- For pixels labeled as parking spaces, merge the line segments on each edge and determine the four vertices of the parking space through the intersection of the lines where the segments lie;
- For semantic categories like no-parking zones, consider fitting lines; if ideal results are not achieved, explore the feasibility of image erosion and other operations;
- For semantic categories such as turning lines and guiding lines that do not exhibit clear linear distributions, consider extracting contour information; specific plans are pending.
Region Growing Algorithm (LSD)
The region growing algorithm in reference to the LSD line segment detection (LSD) algorithm follows the process:

Implementation of region growing in LSD:
/*----------------------------------------------------------------------------*/
/** Build a region of pixels that share the same angle, up to a
tolerance 'prec', starting at point (x,y).
*/
static void region_grow( int x, int y, image_double angles, struct point * reg,
int * reg_size, double * reg_angle, image_char used,
double prec )
{
double sumdx,sumdy;
int xx,yy,i;
/* check parameters */
if( x < 0 || y < 0 || x >= (int) angles->xsize || y >= (int) angles->ysize )
error("region_grow: (x,y) out of the image.");
if( angles == NULL || angles->data == NULL )
error("region_grow: invalid image 'angles'.");
if( reg == NULL ) error("region_grow: invalid 'reg'.");
if( reg_size == NULL ) error("region_grow: invalid pointer 'reg_size'.");
if( reg_angle == NULL ) error("region_grow: invalid pointer 'reg_angle'.");
if( used == NULL || used->data == NULL )
error("region_grow: invalid image 'used'.");
/* first point of the region */
*reg_size = 1;
reg[0].x = x;
reg[0].y = y;
*reg_angle = angles->data[x+y*angles->xsize]; /* region's angle */
sumdx = cos(*reg_angle);
sumdy = sin(*reg_angle);
used->data[x+y*used->xsize] = USED;
/* try neighbors as new region points */
for(i=0; i<*reg_size; i++)
for(xx=reg[i].x-1; xx<=reg[i].x+1; xx++)
for(yy=reg[i].y-1; yy<=reg[i].y+1; yy++)
if( xx>=0 && yy>=0 && xx<(int)used->xsize && yy<(int)used->ysize &&
used->data[xx+yy*used->xsize] != USED &&
isaligned(xx,yy,angles,*reg_angle,prec) )
{
/* add point */
used->data[xx+yy*used->xsize] = USED;
reg[*reg_size].x = xx;
reg[*reg_size].y = yy;
++(*reg_size);
/* update region's angle */
sumdx += cos( angles->data[xx+yy*angles->xsize] );
sumdy += sin( angles->data[xx+yy*angles->xsize] );
*reg_angle = atan2(sumdy,sumdx);
}
}
Semantic Line Segment Fitting for Lane Markings
graph
point_cloud(3D语义点云)
3d2d_proj[3D-2D投影]
2d_point_cloud(2D语义点云)
level_line[局部线性方向与局部线性度计算]
ll_sort[局部线性度伪排序]
region_grow[区域增长]
line_segment(语义线段)
point_cloud --> 3d2d_proj
--> 2d_point_cloud
--> level_line
--> ll_sort
--> region_grow
--> line_segment
Projection of 3D Semantic Point Cloud onto 2D Plane Representation;
Calculation of local linear direction \(\boldsymbol v\) and local linearity \(\gamma\) for semantic points. Specifically, perform PCA analysis on the local point cloud, where the two principal components correspond to eigenvalues \(\lambda_1\) and \(\lambda_2\) with \(\lambda_1\ge \lambda_2\ge0\). The local linear direction \(\boldsymbol v\) is the direction of the eigenvector corresponding to \(\lambda_1\), and the local linearity \(\gamma\) is defined as
Based on the value of local linearity, pseudo-sort the semantic points of a certain class. Specifically, divide into (N) bins based on local linearity and place semantic points into appropriate bins.
Sort semantic points from highest to lowest local linearity, select them as seed points for region growing. Region growing criteria include Euclidean distance between semantic points and consistency between local linear direction and regional linear direction.
Information about line segments within a region is represented by the mean of semantic points \(\boldsymbol\mu_N\) and the regional linear direction \(\boldsymbol v_N\). \(\boldsymbol v_N\) is obtained through eigendecomposition of the region’s covariance matrix \(\boldsymbol C_N\), specifically using the eigenvector corresponding to its largest eigenvalue. During region growing, both \(\boldsymbol\mu_N\) and \(\boldsymbol C_N\) can be updated incrementally.
\[\boldsymbol\mu_{N+1}= \frac{N}{N+1} \left( \boldsymbol\mu_N+ \frac{1}{N}\boldsymbol p_{N+1} \right)\] \[\boldsymbol C_{N+1}= \frac{N}{N+1} \left( \boldsymbol C_{N}+ \frac{1}{N+1} \left(\boldsymbol p_{N+1}-\boldsymbol\mu_N\right) \left(\boldsymbol p_{N+1}-\boldsymbol\mu_N\right)^T \right)\]



Implementation of Semantic Line Segment Fitting
Data Type Definitions
2D Point Cloud Data Type
Encapsulate the 2D point cloud data type CloudData2D, inheriting from the existing type CloudData. Use the pcl::PointXYZI point type to represent 2D points, where the \(z\) coordinate is set to zero, and rename it as POINTXYI. Private pointer for 2D point cloud is defined as a private variable, and methods for handling it are encapsulated within CloudData2D.
Add a member variable local_linearity_ to the 2D point cloud data type CloudData2D, and encapsulate corresponding interfaces for accessing and modifying it.
Introduce a new member variable vec_neighbors_, which stores the indices of neighboring points for each semantic point in the point cloud, and modify relevant interface functions for subsequent region growing processes.
// sensor_data/cloud_data.hpp
class CloudData2D : public CloudData
{
public:
using POINTXYI = CloudData::POINTXYZI;
using CloudData::CLOUD;
using CloudData::CLOUD_PTR;
public:
CloudData2D() : cloud_2d_ptr_(new CLOUD()), local_linearity_(new CLOUD())
{
}
const std::size_t size() const
{
return cloud_2d_ptr_->size();
}
void resize(std::size_t n)
{
cloud_2d_ptr_->resize(n);
}
void clear()
{
cloud_2d_ptr_->clear();
}
POINTXYI &at(std::size_t i)
{
return cloud_2d_ptr_->at(i);
}
const POINTXYI &at(std::size_t i) const
{
return cloud_2d_ptr_->at(i);
}
const POINTXYI &operator[](std::size_t i) const
{
return (*cloud_2d_ptr_)[i];
}
void push_back(POINTXYI pt)
{
pt.z = 0.0;
cloud_2d_ptr_->push_back(pt);
}
void AddPoint(float x, float y, float intensity)
{
POINTXYI pt;
pt.x = x;
pt.y = y;
pt.z = 0.0;
pt.intensity = intensity;
push_back(pt);
}
const CLOUD_PTR &CloudPtr() const
{
return cloud_2d_ptr_;
}
void ResizeLocalLinearity()
{
local_linearity_->resize(cloud_2d_ptr_->size());
vec_neighbors_.resize(cloud_2d_ptr_->size());
}
void AddLocalLinearity(int i, const float &lin, const Eigen::Vector2f &dir, std::vector<int> &neighbors)
{
POINTXYI &pt = local_linearity_->at(i);
pt.x = dir(0);
pt.y = dir(1);
pt.z = lin;
pt.intensity = 0; // unused
vec_neighbors_[i] = neighbors;
}
const float LocalLinearity(int i) const
{
POINTXYI &pt = local_linearity_->at(i);
return pt.z;
}
const Eigen::Vector2f LocalLinearDirection(int i) const
{
POINTXYI &pt = local_linearity_->at(i);
return Eigen::Vector2f(pt.x, pt.y);
}
const bool IsUsed(std::size_t i) const
{
POINTXYI &pt = local_linearity_->at(i);
if (pt.intensity)
return true;
else
return false;
}
void SetStatus(std::size_t i)
{
POINTXYI &pt = local_linearity_->at(i);
pt.intensity = 1;
}
const std::vector<int> &GetNeighbors(size_t idx) const
{
return vec_neighbors_[idx];
}
private:
CLOUD_PTR cloud_2d_ptr_;
// local linearity
// (x,y) local linear direction;
// (z) local linearity value;
// (intensity) status: 0-unused, 1-used;
CLOUD_PTR local_linearity_;
std::vector<std::vector<int>> vec_neighbors_;
};
2D Semantic Point Region Data Type
2D semantic point region stores the indices of semantic points within the region, as well as the mean and covariance of points in the region. During region growing, the mean and covariance of points in the region are incrementally updated, with the update process implemented in the AddPoint function.
In the AddPoint function, an incremental update strategy for the regional linear direction has been added: when the difference between the eigenvalues of the two main directions in the current region is not significant, indicating that the distribution of points in the region does not exhibit clear linear characteristics, the regional linear direction is computed as the mean of the linear directions of all points in the region. However, when there is a significant difference between the two eigenvalues, indicating that the distribution of points in the region exhibits clear linear features, the regional linear direction is set to the principal direction corresponding to the largest eigenvalue.
// models/line_feature_extraction/line_feature_extration_rg.hpp
class Region
{
public:
Region()
{
}
std::size_t &at(std::size_t i)
{
return indices_.at(i);
}
const std::size_t &at(std::size_t i) const
{
return indices_.at(i);
}
const std::size_t &operator[](std::size_t i) const
{
return indices_[i];
}
std::size_t size()
{
return indices_.size();
}
void clear()
{
indices_.clear();
region_centroid_.setZero();
region_covariance_.setZero();
}
std::vector<std::size_t>::iterator begin()
{
return indices_.begin();
}
std::vector<std::size_t>::iterator end()
{
return indices_.end();
}
void AddPoint(const CloudData2D &cloud, std::size_t idx);
const Eigen::Vector2f GetCentroid() const
{
return region_centroid_;
}
const Eigen::Vector2f GetDirection() const
{
return region_direction_;
}
private:
std::vector<std::size_t> indices_;
Eigen::Matrix2f region_covariance_ = Eigen::Matrix2f::Zero();
Eigen::Vector2f region_centroid_ = Eigen::Vector2f::Zero();
Eigen::Vector2f region_direction_ = Eigen::Vector2f::Zero();
};
// models/line_feature_extraction/line_feature_extration_rg.cpp
void Region::AddPoint(const CloudData2D &cloud, std::size_t idx)
{
indices_.push_back(idx);
const CloudData2D::POINTXYI &pt = cloud.at(idx);
Eigen::Vector2f point(pt.x, pt.y);
std::size_t N = indices_.size();
if (N == 1) {
region_centroid_ = point;
region_covariance_.setZero();
region_direction_ = cloud.LocalLinearDirection(idx);
} else {
float ratio = float(N - 1) / float(N);
Eigen::Vector2f tmp = point - region_centroid_;
region_centroid_ = ratio * (region_centroid_ + point / float(N - 1));
region_covariance_ = ratio * (region_covariance_ + tmp * tmp.transpose() / float(N));
Eigen::JacobiSVD<Eigen::Matrix2f> svd(region_covariance_, Eigen::ComputeFullU);
Eigen::Matrix2f U = svd.matrixU();
Eigen::Vector2f D = svd.singularValues();
if (D(1) / D(0) < 0.1) {
region_direction_ = U.block<2, 1>(0, 0);
} else {
region_direction_ = ratio * (region_direction_ + cloud.LocalLinearDirection(idx) / float(N - 1));
}
}
}
Semantic Line Segment Data Type
// sensor_data/line_feature.hpp
class LineFeature2D
{
public:
LineFeature2D() {}
~LineFeature2D() {}
public:
int size = 0;
Eigen::Vector2f startpoint = Eigen::Vector2f::Zero();
Eigen::Vector2f endpoint = Eigen::Vector2f::Zero();
Eigen::Vector2f centroid = Eigen::Vector2f::Zero();
Eigen::Vector2f direction = Eigen::Vector2f::Zero();
Eigen::Matrix2f covariance = Eigen::Matrix2f::Zero();
};
Implementation of Line Segment Extraction Algorithm
Interface Class
Implementation of the semantic line segment extraction interface class:
// models/line_feature_extraction/line_feature_extration_interface.hpp
class LineFeatureExtractionInterface
{
public:
virtual ~LineFeatureExtractionInterface() = default;
virtual bool Extract(const CloudData::CLOUD_PTR &input_cloud) = 0;
// debug
CloudData2D cloud_2d;
protected:
CloudData::CLOUD_PTR input_source_;
};
Functional Class
Functional class implementation of the semantic line segment extraction algorithm based on region growing:
semantic_clouds_2d_ represents a collection of semantic 2D point clouds for semantic line segment extraction. Each point cloud contains points of a specific semantic class. For example, in simulated data, if the semantic categories requiring line segment extraction are parking spaces (label id = 2), lane lines (label id = 4), and center lines (label id = 5), then semantic_clouds_2d_ contains three 2D semantic point clouds.
vec_pseudo_ordering_bins_ and vec_semantic_regions_ correspond to pseudo-sorting bins based on linearity for different semantic point cloud categories and regions generated from region segmentation, respectively.
// models/line_feature_extraction/line_feature_extration_rg.hpp
class LineFeatureExtractionRG : public LineFeatureExtractionInterface
{
public:
using VecBins = std::vector<std::deque<std::size_t>>;
using VecRegion = std::vector<Region>;
LineFeatureExtractionRG(const YAML::Node &node);
bool Extract(const CloudData::CLOUD_PTR &input_cloud) override;
private:
bool Projection3D2D(const CloudData::CLOUD_PTR &cloud_3d, CloudData2D &cloud_2d);
bool ComputeLocalLinearity(CloudData2D &cloud);
bool PseudoOrdering(CloudData2D &cloud, VecBins &pseudo_ordering_bins);
bool RegionSegmentation(CloudData2D &cloud, VecBins &pseudo_ordering_bins, std::vector<Region> ®ions);
bool RegionGrow(CloudData2D &cloud, std::size_t seed_idx, Region ®ion);
float AngleDiff(const Eigen::Vector2f &dir1, const Eigen::Vector2f &dir2);
private:
int num_neighbors_svd_ = 10;
float local_direction_threshold_ = 0.52; // 30deg
int region_size_threshold_ = 20;
std::vector<CloudData2D> semantic_clouds_2d_;
std::vector<VecBins> vec_pseudo_ordering_bins_;
std::vector<VecRegion> vec_semantic_regions_;
// pseudo_ordering_bins_
// [0.0,0.1),[0.1,0.2),...,[0.9,1.0];
//std::vector<std::deque<std::size_t>> pseudo_ordering_bins_;
//std::vector<Region> cloud_2d_regions_;
};
3D-2D Projection of Semantic Point Clouds
The functionality for projecting semantic point clouds from 3D to 2D, implemented as Projection3D2D function, outputs data in the defined data type CloudData2D.
The input parameter label_id corresponds to the semantic label ID. The output point cloud cloud stores the 2D projection of points from cloud_3d where the semantic label is label_id.
// models/line_feature_extraction/line_feature_extration_rg.hpp
bool LineFeatureExtractionRG::Projection3D2D(const CloudData::CLOUD_PTR &cloud_3d, const int label_id,
CloudData2D &cloud)
{
if (cloud_3d->size() < 10) {
ERROR("[LineFeatureExtractionRG][Projection3D2D] empty input 3d cloud!");
return false;
}
cloud.clear();
for (auto it_pt = cloud_3d->begin(); it_pt != cloud_3d->end(); ++it_pt) {
const CloudData::POINTXYZI &pt = *it_pt;
if (floorf(pt.intensity) == label_id) cloud.AddPoint(pt.x, pt.y, pt.intensity);
}
return true;
}
Calculation of Local Linearity and Local Linear Direction for Semantic Point Clouds
Function ComputeLocalLinearity computes the local linearity and local linear direction for each point in the semantic point cloud. It performs \( K \)-nearest neighbor search, where the number of neighbors is defined by the private variable num_neighbors_svd_, which can be configured in the config file. PCA analysis is applied to the nearest neighbors to determine the principal direction as the local linear direction, and calculates the local linearity. Results are stored in the 2D point cloud structure CloudData2D.
bool LineFeatureExtractionRG::ComputeLocalLinearity(CloudData2D &cloud)
{
if (cloud.size() < 10) {
ERROR("[LineFeatureExtractionRG][LocalLinearity] empty input point cloud!");
return false;
}
pcl::PointCloud<pcl::PointXY>::Ptr cloud_kdtree(new pcl::PointCloud<pcl::PointXY>);
pcl::KdTreeFLANN<pcl::PointXY>::Ptr kdtree_ptr(new pcl::KdTreeFLANN<pcl::PointXY>);
cloud_kdtree->resize(cloud.size());
for (std::size_t i = 0; i < cloud.size(); i++) {
cloud_kdtree->at(i).x = cloud.at(i).x;
cloud_kdtree->at(i).y = cloud.at(i).y;
}
kdtree_ptr->setInputCloud(cloud_kdtree);
std::vector<int> nn_indices;
std::vector<float> nn_dist_sq;
nn_indices.reserve(num_neighbors_svd_);
nn_dist_sq.reserve(num_neighbors_svd_);
Eigen::Vector2f mu;
Eigen::Matrix2f cov;
cloud.ResizeLocalLinearity();
for (std::size_t i = 0; i < cloud.size(); i++) {
const pcl::PointXY &query = cloud_kdtree->at(i);
kdtree_ptr->nearestKSearch(query, num_neighbors_svd_, nn_indices, nn_dist_sq);
mu.setZero();
cov.setZero();
for (std::size_t j = 0; j < nn_indices.size(); j++) {
const pcl::PointXY &pt = cloud_kdtree->at(nn_indices[j]);
mu(0) += pt.x;
mu(1) += pt.y;
cov(0, 0) += pt.x * pt.x;
cov(1, 0) += pt.y * pt.x;
cov(1, 1) += pt.y * pt.y;
}
mu /= static_cast<float>(num_neighbors_svd_);
for (int k = 0; k < 2; k++) {
for (int l = 0; l <= k; l++) {
cov(k, l) /= static_cast<float>(num_neighbors_svd_);
cov(k, l) -= mu[k] * mu[l];
cov(l, k) = cov(k, l);
}
}
Eigen::JacobiSVD<Eigen::Matrix2f> svd(cov, Eigen::ComputeFullU);
Eigen::Matrix2f U = svd.matrixU();
Eigen::Vector2f val = svd.singularValues(); // sorted in decreasing order;
float lin = 1.0 - val(1) / val(0);
Eigen::Vector2f dir(U(0, 0), U(1, 0));
cloud.AddLocalLinearity(i, lin, dir, nn_indices);
}
return true;
}
Pseudo-Sorting Based on Local Linearity
Local linearity \(\gamma\in[0,1]\) is divided into 10 bins. Based on the value of local linearity, 2D semantic points are placed into corresponding bins.
bool LineFeatureExtractionRG::PseudoOrdering(CloudData2D &cloud, VecBins &pseudo_ordering_bins)
{
if (cloud.size() < 10) {
ERROR("[LineFeatureExtractionRG][PseudoOrdering] empty input point cloud!");
return false;
}
pseudo_ordering_bins.resize(10);
for (std::size_t i = 0; i < pseudo_ordering_bins.size(); i++) {
pseudo_ordering_bins[i].clear();
}
for (std::size_t i = 0; i < cloud.size(); i++) {
int idx = floorf(cloud.LocalLinearity(i) * 10.0);
if (idx > 9) idx = 9;
pseudo_ordering_bins[idx].push_back(i);
}
return true;
}
Region Growing Algorithm
Region growing algorithm used in the LSD algorithm, where the growth condition is the consistency between the local linear direction and the regional linear direction.
bool LineFeatureExtractionRG::RegionSegmentation(CloudData2D &cloud, VecBins &pseudo_ordering_bins, std::vector<Region> ®ions)
{
cloud_2d_regions_.clear();
for (std::size_t i = 0; i < pseudo_ordering_bins.size(); i++) {
for (auto it = pseudo_ordering_bins[i].begin(); it != pseudo_ordering_bins[i].end(); ++it) {
const std::size_t seed_idx = *it;
if (cloud.IsUsed(seed_idx)) continue;
Region reg;
if (RegionGrow(cloud, seed_idx, reg)) cloud_2d_regions_.push_back(reg);
}
}
return true;
}
bool LineFeatureExtractionRG::RegionGrow(CloudData2D &cloud, std::size_t seed_idx, Region ®ion)
{
if (seed_idx < 0 || seed_idx >= cloud.size()) {
ERROR("[LineFeatureExtractionRG][RegionGrow] wrong seed point index!");
return false;
}
region.clear();
region.AddPoint(cloud, seed_idx);
for (std::size_t i = 0; i < region.size(); i++) {
std::size_t idx = region[i];
const std::vector<int> &neighbors = cloud.GetNeighbors(idx);
for (auto itn = neighbors.begin(); itn != neighbors.end(); ++itn) {
std::size_t idxn = *itn;
if (cloud.IsUsed(idxn)) continue;
Eigen::Vector2f region_dir = region.GetDirection();
Eigen::Vector2f point_dir = cloud.LocalLinearDirection(idxn);
if (AngleDiff(region_dir, point_dir) < local_direction_threshold_) {
region.AddPoint(cloud, idxn);
cloud.SetStatus(idxn);
}
}
}
if (region.size() < region_size_threshold_)
return false;
else
return true;
}
float LineFeatureExtractionRG::AngleDiff(const Eigen::Vector2f &dir1, const Eigen::Vector2f &dir2)
{
return acos(fabs(dir1.dot(dir2)));
}
Interface Function
In the interface function Extract, the functionality for semantic line segment extraction is tested.
bool LineFeatureExtractionRG::Extract(const CloudData::CLOUD_PTR &input_cloud)
{
std::vector<int> labels;
labels.push_back(2); // parking lot
labels.push_back(4); // lane
labels.push_back(5); // lane center line
const std::size_t N = labels.size();
semantic_clouds_2d_.resize(N);
vec_pseudo_ordering_bins_.resize(N);
vec_semantic_regions_.resize(N);
cloud_2d.clear();
for (std::size_t i = 0; i < labels.size(); i++) {
Projection3D2D(input_cloud, labels[i], semantic_clouds_2d_[i]);
if (semantic_clouds_2d_[i].size() < 10) continue;
ComputeLocalLinearity(semantic_clouds_2d_[i]);
PseudoOrdering(semantic_clouds_2d_[i], vec_pseudo_ordering_bins_[i]);
RegionSegmentation(semantic_clouds_2d_[i], vec_pseudo_ordering_bins_[i], vec_semantic_regions_[i]);
// DEBUG
for (std::size_t j = 0; j < semantic_clouds_2d_[i].size(); j++) {
CloudData2D::POINTXYI &pt = semantic_clouds_2d_[i].at(j);
if (!semantic_clouds_2d_[i].IsUsed(j)) pt.intensity = -1;
}
for (std::size_t r = 0; r < vec_semantic_regions_[i].size(); r++) {
for (std::size_t k = 0; k < vec_semantic_regions_[i][r].size(); k++) {
std::size_t idx = vec_semantic_regions_[i][r].at(k);
CloudData2D::POINTXYI &ptt = semantic_clouds_2d_[i].at(idx);
ptt.intensity = r + 1;
}
}
// DEBUG
for (std::size_t j = 0; j < semantic_clouds_2d_[i].size(); j++) {
CloudData2D::POINTXYI &pt = semantic_clouds_2d_[i].at(j);
cloud_2d.AddPoint(pt.x, pt.y, pt.intensity);
}
}
return true;
}
Semantic Line Matching
LOAM Matching Method Based on Local Line-to-Plane Features
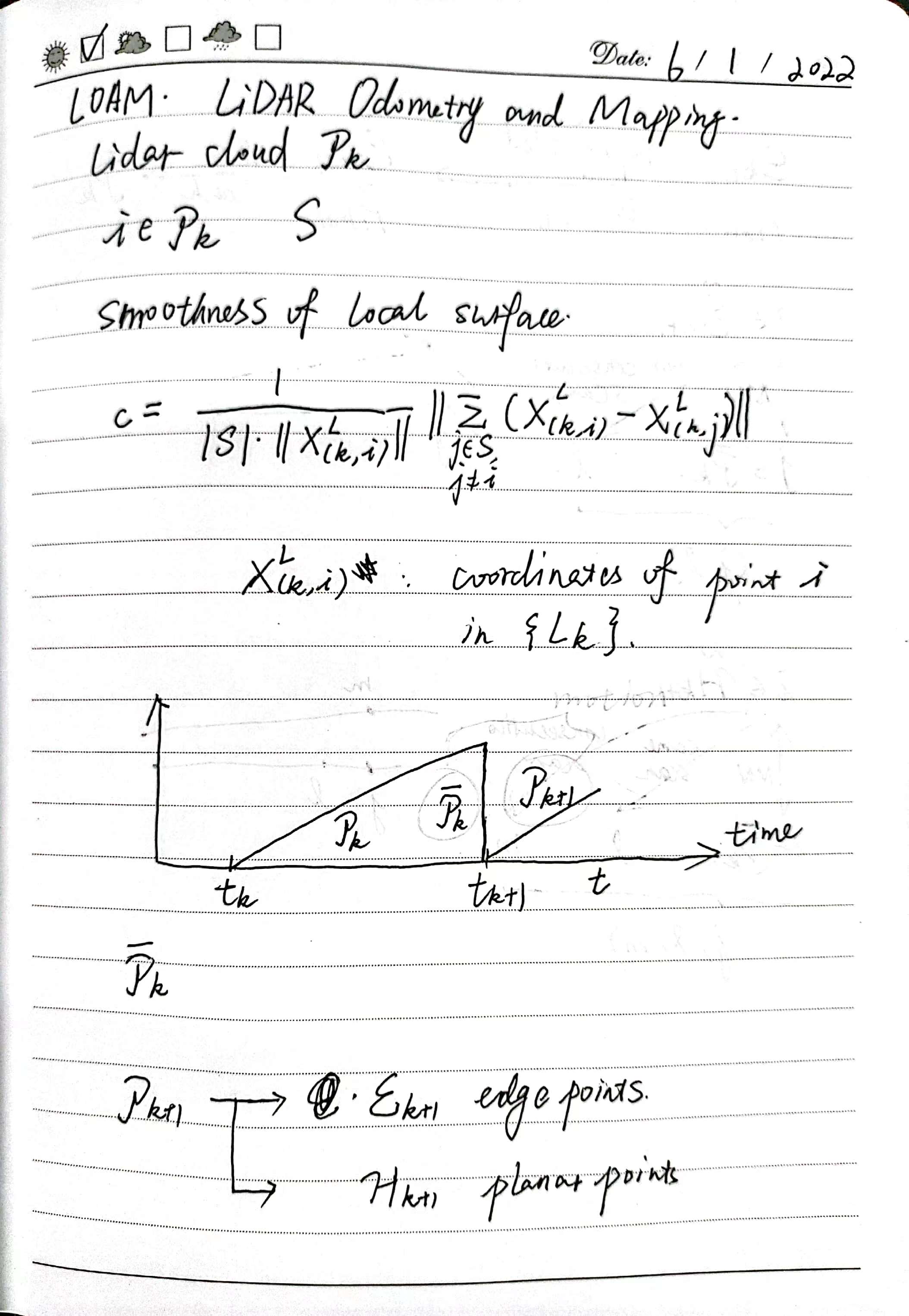
In LOAM odometry, the distance function from point to line is defined as
\[d_{\mathcal E}= \frac{ \left| \left(\tilde{\boldsymbol X}^L_{(k+1,i)}-\bar{\boldsymbol X}^L_{(k,j)}\right) \times \left(\tilde{\boldsymbol X}^L_{(k+1,i)}-\bar{\boldsymbol X}^L_{(k,j)}\right) \right|} {\bar{\boldsymbol X}^L_{(k,j)}-\bar{\boldsymbol X}^L_{(k,j)}}\]The geometric meaning of the above equation is the perpendicular distance from point \(\tilde{\boldsymbol X}^L_{(k+1,i)}\) to the line segment formed by \(\bar{\boldsymbol X}^L_{(k,j)}\) and \(\bar{\boldsymbol X}^L_{(k,j)}\).

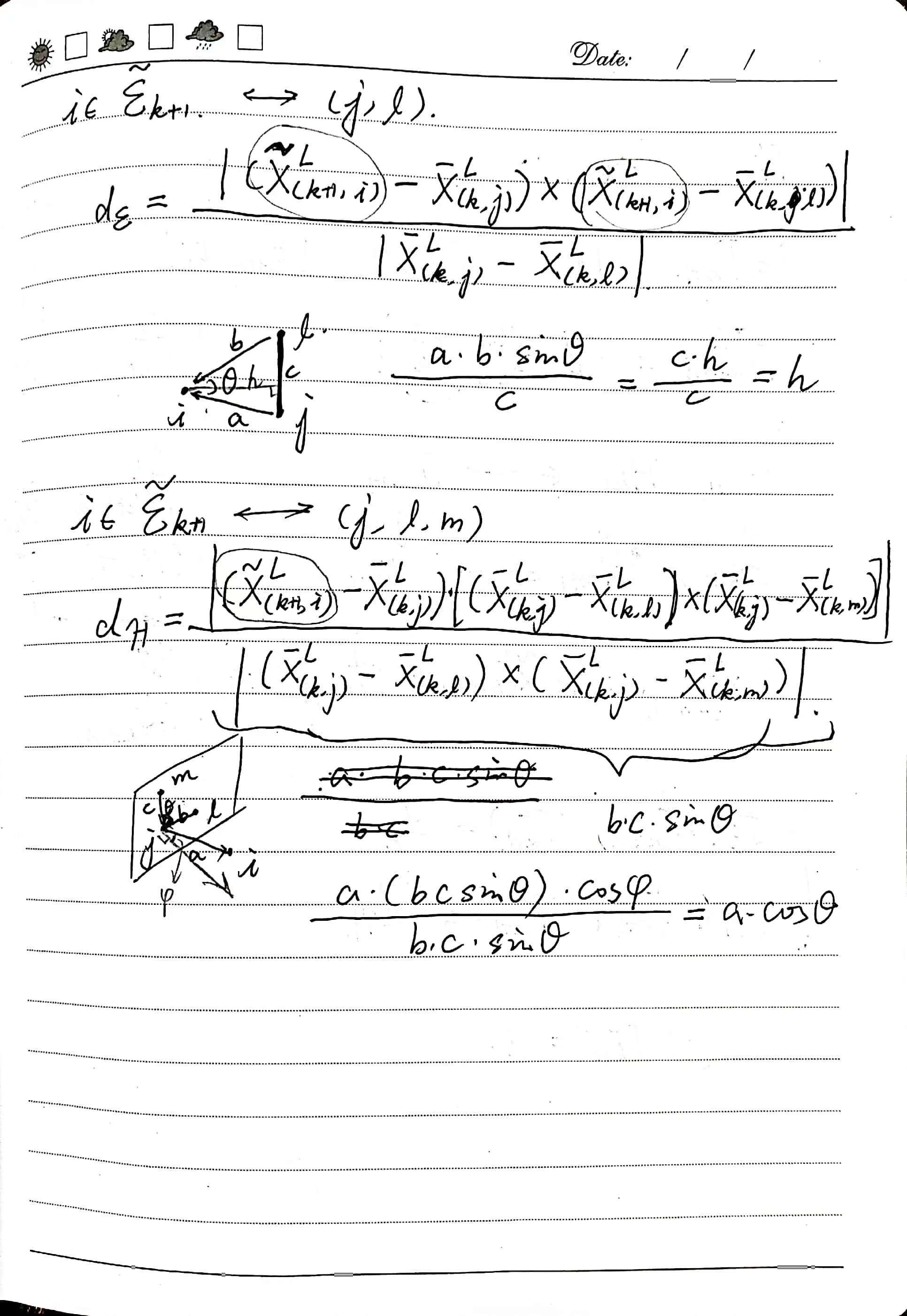

Parametrization Method for Semantic Line Segments
A semantic line segment \(\mathcal{L}\) is represented as:
\[\mathcal{L}=(\boldsymbol p_c,\boldsymbol d,\boldsymbol p_{e1},\boldsymbol p_{e2},s,id)\]where \(\boldsymbol p_c\) represents the coordinates of the line segment’s center point, \(\boldsymbol d\) denotes the direction vector of the line segment, \(\boldsymbol p_{e1}\) and \(\boldsymbol p_{e2}\) are the coordinates of the two endpoints of the line segment, \(s\) indicates the number of semantic points used for fitting the line segment, and \(id\) is the semantic label of the line segment.
Establishment of Correspondence
Point-to-point nearest neighbor search using KdTree is employed to find the nearest points under the current semantic label. Then, the closest semantic line segment in the target point cloud is determined, using the perpendicular distance from the current query point to the semantic line segment found in the objective function.
During semantic line segment extraction, it’s necessary to maintain index information linking semantic points to semantic line segments.
Derivation of Jacobian Matrix
The optimization objective function is defined as
\[F(\boldsymbol\xi)= \sum^N_{i=1}d_{\mathcal{E}i}= \sum^N_{i=1} \frac{ \left| (\boldsymbol p'_i-\boldsymbol p_{e1,i})\times (\boldsymbol p'_i-\boldsymbol p_{e2,i}) \right| }{ \left| \boldsymbol p_{e1,i}-\boldsymbol p_{e2,i} \right| }\]其中
\[\boldsymbol p'_i=\boldsymbol R\boldsymbol p_i+\boldsymbol t\]The specific derivation process of the Jacobian \(\frac{\partial F}{\partial\xi}\) is as follows.



Translation:
Euclidean Distance (Gradient) Field
In motion planning based on gradient information, the Euclidean Signed Distance Field (ESDF) is commonly used to represent space. It directly provides distance and gradient information from a point in space to obstacles.
Paragraph from the paper “CHOMP: Gradient Optimization Techniques for Efficient Motion Planning”:
If obstacles are static and the description of B is geometrically simple, it becomes advantageous to simply precompute a signed distance field $d(x)$ which stores the distance from a point $x\in\mathbb{R}^3$ to the boundary of the nearest obstacle. Values of $d(x)$ are negative inside obstacles, positive outside, and zero at the boundary.
Computing $d(x)$ on a uniform grid is straightforward. We start with a boolean-valued voxel representation of the environment, and compute the Euclidean Distance Transform
(EDT) for both the voxel map and its logical complement. The signed distance field is then simply given by the difference of the two EDT values. Computing the EDT is surprisingly efficient: for a lattice of $K$ samples, computation takes time $O(K)$ [10].
Read the paper “Distance Transforms of Sampled Functions”.



Implementation of Semantic Line Segment Matching
Semantic Line Segment Extraction from Target Point Cloud
Based on semantic labels, the input target point cloud is grouped, and semantic line segments are extracted for each semantic class. Simultaneously, indices of points to semantic line segments are obtained. In the function CloudClassify, only three semantic label point clouds suitable for line segment fitting are selected for matching: lane lines, center lines, and parking spaces. In the current version, point clouds with other class labels are not included in the computation.
// models/registration/plicp_registration.cpp
bool PLICPRegistration::SetInputTarget(const CloudData::CLOUD_PTR &input_target)
{
CloudClassify(input_target, input_target_group_,
input_target_group_kdtree_, input_target_group_empty_);
input_target_group_lines_.resize(input_target_group_.size());
input_target_group_lines_indices_.resize(input_target_group_.size());
for (std::size_t i = 0; i < input_target_group_.size(); i++) {
if (input_target_group_empty_[i]) continue;
line_extract_ptr_->Extract(input_target_group_[i], i,
input_target_group_lines_[i],
input_target_group_lines_indices_[i]);
}
return true;
}
Here are the output interfaces of the semantic line segment extraction functional class:
// models/line_feature_extraction/line_feature_extraction_rg.cpp
bool LineFeatureExtractionRG::Extract(const CloudData::CLOUD_PTR &input_cloud,
const int semantic_id,
std::vector<LineFeature> &lines,
std::vector<int> &indices)
{
lines.clear();
indices.resize(input_cloud->size(), -1);
Projection3D2D(input_cloud, semantic_id, semantic_clouds_2d_);
if (semantic_clouds_2d_.size() < 10) continue;
ComputeLocalLinearity(semantic_clouds_2d_);
PseudoOrdering(semantic_clouds_2d_, vec_pseudo_ordering_bins_);
RegionSegmentation(semantic_clouds_2d_, vec_pseudo_ordering_bins_,
vec_semantic_regions_);
for (std::size_t r = 0; r < vec_semantic_regions_.size(); r++) {
Region ®ion = vec_semantic_regions_[r];
LineFeature line;
region.ToLineFeature(semantic_clouds_2d_, semantic_id, line);
lines.push_back(line);
for (std::size_t k = 0; k < region.size(); k++) {
std::size_t idx = region.at(k);
indices[idx] = lines.size() - 1;
}
}
return true;
}
Objective Function and Jacobian Function in Nonlinear Optimization
Implement relevant functions in nonlinear optimization based on the definition of the objective function and the derived form of the Jacobian matrix.
// models/registration/plicp_registration.cpp
inline double PLICPRegistration::OptimizationFunctor::operator()(const Vector6f &x)
{
Eigen::Isometry3f transformation_matrix = Eigen::Isometry3f::Identity();
plicp_->ApplyState(transformation_matrix, x);
float f = 0;
int N = 0;
for (int k = 0; k < plicp_->SEMANTIC_NUMS; k++) {
int m = static_cast<int>((*plicp_->tmp_idx_src_)[k].size());
for (int i = 0; i < m; ++i) {
int idx_src = (*plicp_->tmp_idx_src_)[k][i];
int idx_tgt = (*plicp_->tmp_idx_tgt_)[k][i];
CloudData::POINTXYZI pt_src = (*plicp_->tmp_src_)[k]->points[idx_src];
Eigen::Vector3f p_src(pt_src.x, pt_src.y, pt_src.z);
Eigen::Vector3f pp(transformation_matrix * p_src);
int idx_line = (*plicp_->tmp_idx_lines_tgt_)[k][idx_tgt];
Eigen::Vector3f ep_1 = (*plicp_->tmp_lines_tgt_)[k][idx_line].endpoint_1;
Eigen::Vector3f ep_2 = (*plicp_->tmp_lines_tgt_)[k][idx_line].endpoint_2;
Eigen::Vector3f tmp_1 = pp - ep_1;
Eigen::Vector3f tmp_2 = pp - ep_2;
Eigen::Vector3f den = ep_1 - ep_2;
f += float(tmp_1.cross(tmp_2).norm() / den.norm());
}
N += m;
}
return f / float(N);
}
inline void PLICPRegistration::OptimizationFunctor::df(const Vector6f &x,
Vector6f &g)
{
Eigen::Isometry3f transformation_matrix = Eigen::Isometry3f::Identity();
plicp_->ApplyState(transformation_matrix, x);
g.setZero();
Eigen::Matrix3f R = Eigen::Matrix3f::Zero();
int N = 0;
for (int k = 0; k < plicp_->SEMANTIC_NUMS; k++) {
int m = static_cast<int>((*plicp_->tmp_idx_src_)[k].size());
for (int i = 0; i < m; ++i) {
int idx_src = (*plicp_->tmp_idx_src_)[k][i];
int idx_tgt = (*plicp_->tmp_idx_tgt_)[k][i];
CloudData::POINTXYZI pt_src = (*plicp_->tmp_src_)[k]->points[idx_src];
Eigen::Vector3f p_src(pt_src.x, pt_src.y, pt_src.z);
Eigen::Vector3f pp(transformation_matrix * p_src);
int idx_line = (*plicp_->tmp_idx_lines_tgt_)[k][idx_tgt];
Eigen::Vector3f ep_1 = (*plicp_->tmp_lines_tgt_)[k][idx_line].endpoint_1;
Eigen::Vector3f ep_2 = (*plicp_->tmp_lines_tgt_)[k][idx_line].endpoint_2;
Eigen::Vector3f tmp_1 = pp - ep_1;
Eigen::Vector3f tmp_2 = pp - ep_2;
Eigen::Vector3f pc = tmp_1.cross(tmp_2);
Eigen::Vector3f den = ep_1 - ep_2;
float Lle = pc.norm() * den.norm();
Eigen::Vector3f ddE_dt;
ddE_dt[0] = (pc[1] * (ep_2[2] - ep_1[2]) + pc[2] * (ep_1[1] - ep_2[1])) / Lle;
ddE_dt[1] = (pc[0] * (ep_1[2] - ep_2[2]) + pc[2] * (ep_2[0] - ep_1[0])) / Lle;
ddE_dt[2] = (pc[0] * (ep_2[1] - ep_1[1]) + pc[1] * (ep_1[0] - ep_2[0])) / Lle;
g.head<3>() += ddE_dt;
Eigen::Matrix3f dP_dtheta;
plicp_->ComputeRDerivative(x, pp, dP_dtheta);
g.tail<3>() += ddE_dt.transpose() * dP_dtheta;
}
N += m;
}
g /= float(N);
}
inline void PLICPRegistration::OptimizationFunctor::fdf(const Vector6f &x,
float &f, Vector6f &g)
{
Eigen::Isometry3f transformation_matrix = Eigen::Isometry3f::Identity();
plicp_->ApplyState(transformation_matrix, x);
f = 0;
g.setZero();
Eigen::Matrix3f R = Eigen::Matrix3f::Zero();
int N = 0;
for (int k = 0; k < plicp_->SEMANTIC_NUMS; k++) {
int m = static_cast<int>((*plicp_->tmp_idx_src_)[k].size());
for (int i = 0; i < m; ++i) {
int idx_src = (*plicp_->tmp_idx_src_)[k][i];
int idx_tgt = (*plicp_->tmp_idx_tgt_)[k][i];
CloudData::POINTXYZI pt_src = (*plicp_->tmp_src_)[k]->points[idx_src];
Eigen::Vector3f p_src(pt_src.x, pt_src.y, pt_src.z);
Eigen::Vector3f pp(transformation_matrix * p_src);
int idx_line = (*plicp_->tmp_idx_lines_tgt_)[k][idx_tgt];
Eigen::Vector3f ep_1 = (*plicp_->tmp_lines_tgt_)[k][idx_line].endpoint_1;
Eigen::Vector3f ep_2 = (*plicp_->tmp_lines_tgt_)[k][idx_line].endpoint_2;
Eigen::Vector3f tmp_1 = pp - ep_1;
Eigen::Vector3f tmp_2 = pp - ep_2;
Eigen::Vector3f den = ep_1 - ep_2;
f += float(tmp_1.cross(tmp_2).norm() / den.norm());
Eigen::Vector3f pc = tmp_1.cross(tmp_2);
float Lle = pc.norm() * den.norm();
Eigen::Vector3f ddE_dt;
ddE_dt[0] = (pc[1] * (ep_2[2] - ep_1[2]) + pc[2] * (ep_1[1] - ep_2[1])) / Lle;
ddE_dt[1] = (pc[0] * (ep_1[2] - ep_2[2]) + pc[2] * (ep_2[0] - ep_1[0])) / Lle;
ddE_dt[2] = (pc[0] * (ep_2[1] - ep_1[1]) + pc[1] * (ep_1[0] - ep_2[0])) / Lle;
g.head<3>() += ddE_dt;
Eigen::Matrix3f dP_dtheta;
plicp_->ComputeRDerivative(x, pp, dP_dtheta);
g.tail<3>() += ddE_dt.transpose() * dP_dtheta;
}
N += m;
}
f /= float(N);
g /= float(N);
}
Code Debugging
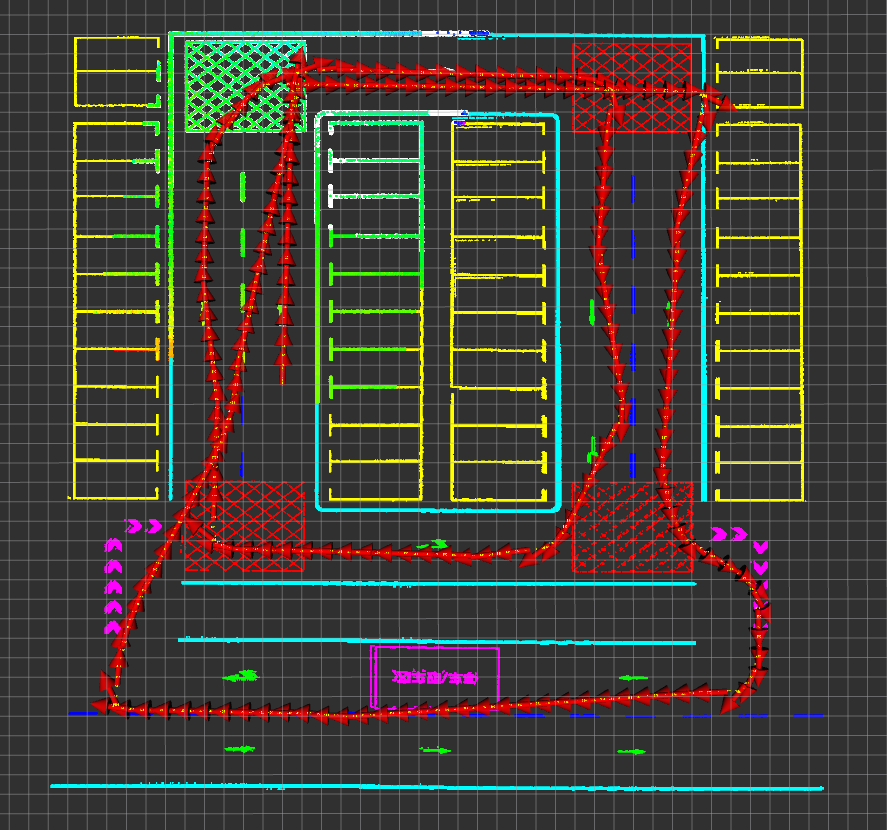
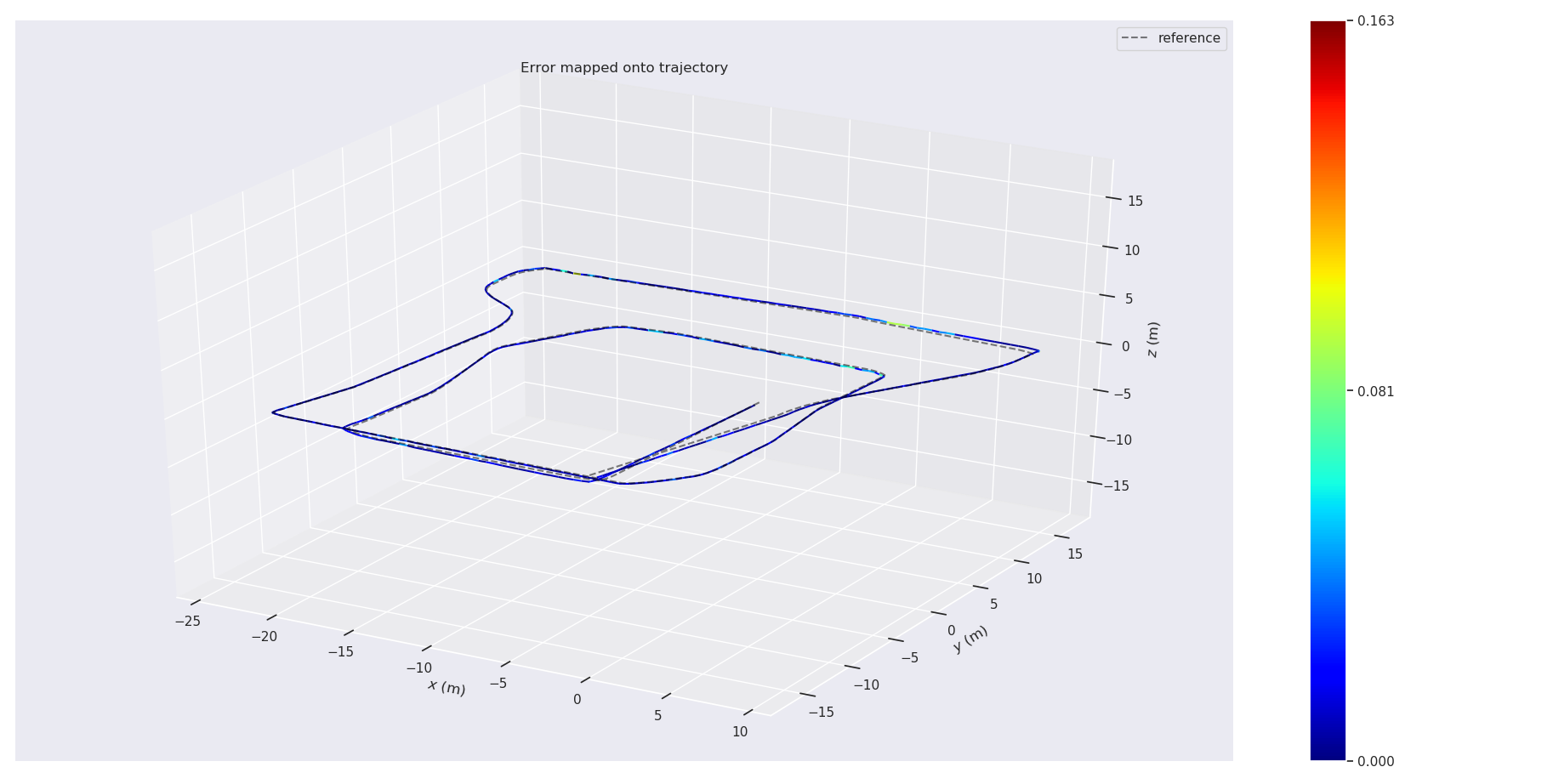
Parameter debugging for the semantic line segment-based matching method (PL-ICP), with evaluation results as follows.
| RPE RMSE (vo) | APE RMSE (optimized) | |
|---|---|---|
| plicp 1 | 0.027101 | 0.080187 |
| plicp 2 | 0.023345 | 0.072611 |
| plicp 3 | 0.022827 | 0.105105 |
| plicp 4 | 0.024279 | 0.083953 |
| plicp 5 | 0.024362 | 0.100988 |
| plicp 6 | 0.024908 | 0.067737 |
| plicp 7 | 0.024397 | 0.064946 |
| plicp 8 | 0.022378 | 0.065225 |
| plicp 9 | 0.021367 | 0.086566 |
The parameter configurations corresponding to each row of the table above are as follows:
plicp 1:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.1, 0.3]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.3
local_direction_threshold: 30 #deg
region_size_threshold: 20
plicp 2:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.2, 0.5]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.3
local_direction_threshold: 30 #deg
region_size_threshold: 20
plicp 3:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.2, 0.5]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.3
local_direction_threshold: 30 #deg
region_size_threshold: 30
plicp 4:
fit_eps : 1e-3
trans_eps : 1e-5
corr_dist : [0.2, 0.5]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.3
local_direction_threshold: 30 #deg
region_size_threshold: 30
plicp 5:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.2, 0.5]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.3
local_direction_threshold: 20 #deg
region_size_threshold: 20
plicp 6:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.3, 0.6]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.3
local_direction_threshold: 30 #deg
region_size_threshold: 20
plicp 7:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.3, 0.6]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.2
local_direction_threshold: 20 #deg
region_size_threshold: 30
plicp 8:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.3, 0.6]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.2
local_direction_threshold: 20 #deg
region_size_threshold: 20
plicp 9:
fit_eps : 1e-4
trans_eps : 1e-6
corr_dist : [0.2, 0.5]
max_iter : 30
# semantic line segment extraction
line_feature_extraction_method: region_grow
line_region_grow:
num_neighbors_svd: 20
radius_neighbors_svd: 0.2
local_direction_threshold: 30 #deg
region_size_threshold: 20
Related Links
code: