Misalignment Error Computation
Date:
The measurement model is given by
\[\boldsymbol{y}_{k}^m=D\boldsymbol{m}_k^m+\boldsymbol{o}\] \[\boldsymbol{y}_{k}^m=DR^{mb}R_k^{bn}\boldsymbol{m}_k^{n}+\boldsymbol{o}\]Form a small rotation perturbation on the left of the “base” alignment rotation.
\[\boldsymbol{y}_{k}^m=D\exp(\phi^\wedge)\bar{R}^{mb}\boldsymbol{m}_k^{b}+\boldsymbol{o}\]According to the relative orientation of the sensors, the “base” alignment rotation can be approximated by
\[\bar{R}^{mb}= \begin{bmatrix} -1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{bmatrix}\]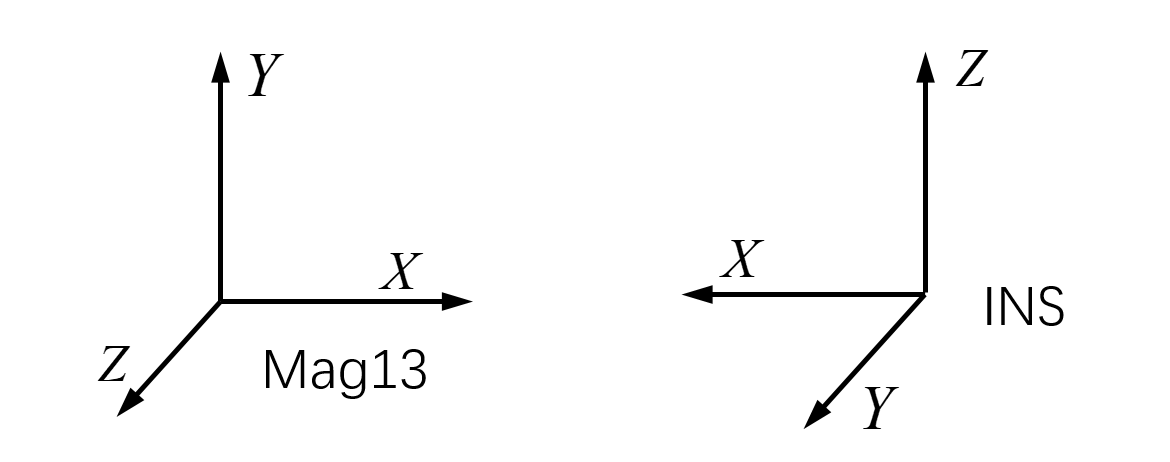
Compute the partial derivative of the measurement model w.r.t. the angle perturbation.
\[\frac{\partial\boldsymbol y^m_k}{\partial\boldsymbol\phi}= D\frac{\partial}{\partial\boldsymbol\phi} \left( \exp(\phi^\wedge)\bar{R}^{mb}\boldsymbol{m}_k^{b} \right)\]Compute the derivative along the directions of each basis \(\phi_i\boldsymbol 1_i\).
\[\begin{aligned} \frac{\partial\boldsymbol y^m_k}{\partial\phi_i} &=\lim_{h\rightarrow 0}D \frac{\exp(h\boldsymbol 1_i^\wedge)\bar{R}^{mb}\boldsymbol{m}_k^{b}-\bar{R}^{mb}\boldsymbol{m}_k^{b}}{h} \\ &=\lim_{h\rightarrow 0}D \frac{(\boldsymbol I+h\boldsymbol 1_i^\wedge)\bar{R}^{mb}\boldsymbol{m}_k^{b}-\bar{R}^{mb}\boldsymbol{m}_k^{b}}{h} \\ &=\lim_{h\rightarrow 0}D \frac{h\boldsymbol 1_i^\wedge(\bar{R}^{mb}\boldsymbol{m}_k^{b})}{h} \\ &=D\boldsymbol 1_i^\wedge(\bar{R}^{mb}\boldsymbol{m}_k^{b}) \\ &=-D(\bar{R}^{mb}\boldsymbol{m}_k^{b})^\wedge\boldsymbol 1_i \\ \end{aligned}\]Stacking the three directional derivatives together yields
\[\frac{\partial\boldsymbol y^m_k}{\partial\boldsymbol\phi}= -D(\bar{R}^{mb}\boldsymbol{m}_k^{b})^\wedge\]Note that, as described here, the model coefficients \(D\) cannot be obtained directly. So it is approximated by
\[D=\tilde DV\approx\tilde D\hat R(\bar R^{mb})^T\]The final result is
\[\frac{\partial\boldsymbol y^m_k}{\partial\boldsymbol\phi}= -\tilde D\hat R(\bar R^{mb})^T(\bar{R}^{mb}\boldsymbol{m}_k^{b})^\wedge\]