相关方法调研与分析

research journal, 2015.09.

九月份之前实验进展及遇到问题概述

实验进展

用逐层分割后每个叶子节点的均值来表示降采样后的一个点的坐标，以欧式距离为优化目标进行匹配时，效果较均匀降采样有所提升。提升的程度根据扫描帧的差异有所不同。

这里所采用的误差计算方法：用图像平面的特征点投影到三维空间得到的三维特征点，来计算均方误差，以此来比较当前方法与原有方法相比是否有所提升。但这种误差计算方法是有问题的，个人以为只能勉强作为评定优劣的标准，不能做为论文中的实验结果数据来呈现。

遇到问题

在此基础上，若加上逐层分割后得到的叶子节点的法向量信息（即协方差信息），以马氏距离为优化目标进行匹配时，效果较均匀降采样没有显著提升。

针对此问题，又对当前方法得到的法向量信息进行简单可视化，发现与基于局部拟合相似，基于点集分割得到的法向量依然不能很好地表征点云的表面信息。

关于量化实验结果的问题

由于现在为止跑实验所用的数据集都是家服上采集的，没有groundtruth，所以在误差计算的时候用的都是匹配之后对应点的平均距离，而对应点的选取用的是图像平面匹配好的特征点在三维空间的投影，因为在ICP的过程中，每一次迭代都是要重新进行对应点的计算，如果用ICP中所计算出的对应点信息，受匹配算法本身的影响太大。

而论文中最后的实验结果呈现，我觉得还是需要用标记过groundtruth的数据集，通过定位误差的计算来表征扫描匹配的结果，这样更具有说服力吧？

九月份期间针对遇到问题所做猜想、调研和分析

Kinect深度数据分析调研¹

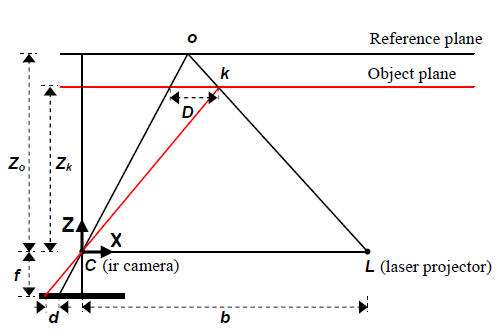
Kinect的深度信息\(Z_k\)是根据disparity image \(d\)计算出来的，其关系满足

假设\(d\)满足正态分布，其方差为\(\sigma_d\)，则可知深度\(Z_k\)的方差为

由此可知深度信息的不确定度与深度值是平方增加的关系，这与我之前在实验中直观得到的结论恰好一致。（之前在实验中为点集分割设置阈值的时候发现，阈值设置与深度的平方正相关时，视觉上看到的采样结果是最好的）

同理，由深度信息计算得到三维点坐标的方法可知，对于三维点云中的每一个点，三个轴方向的不确定度都符合这一规律。再结合之前拟合法向量的可视化效果，距离Kinect越远的点拟合效果越差，应该就是与深度数据的这一特点直接相关。

当前方法与GICP算法比较²

在GICP算法中，假设点云中的每个点都服从高斯分布\(\mathcal{N}(\mu,\Sigma)\)，\(\mu\)即该点坐标，而\(\Sigma\)是用\(k\)个最近邻点来估算的，而迭代过程中点与点的对应关系是通过最小欧式距离来计算的，其优化目标是对应点对的平均马氏距离。

但GICP算法的提出是针对激光数据，首先其相对于Kinect来说准确性更高，另外也没有随深度增加精度下降的问题，所以GICP的运用可以得到比标准ICP更好的效果，但若将其直接应用于Kinect数据，我认为是有问题的。

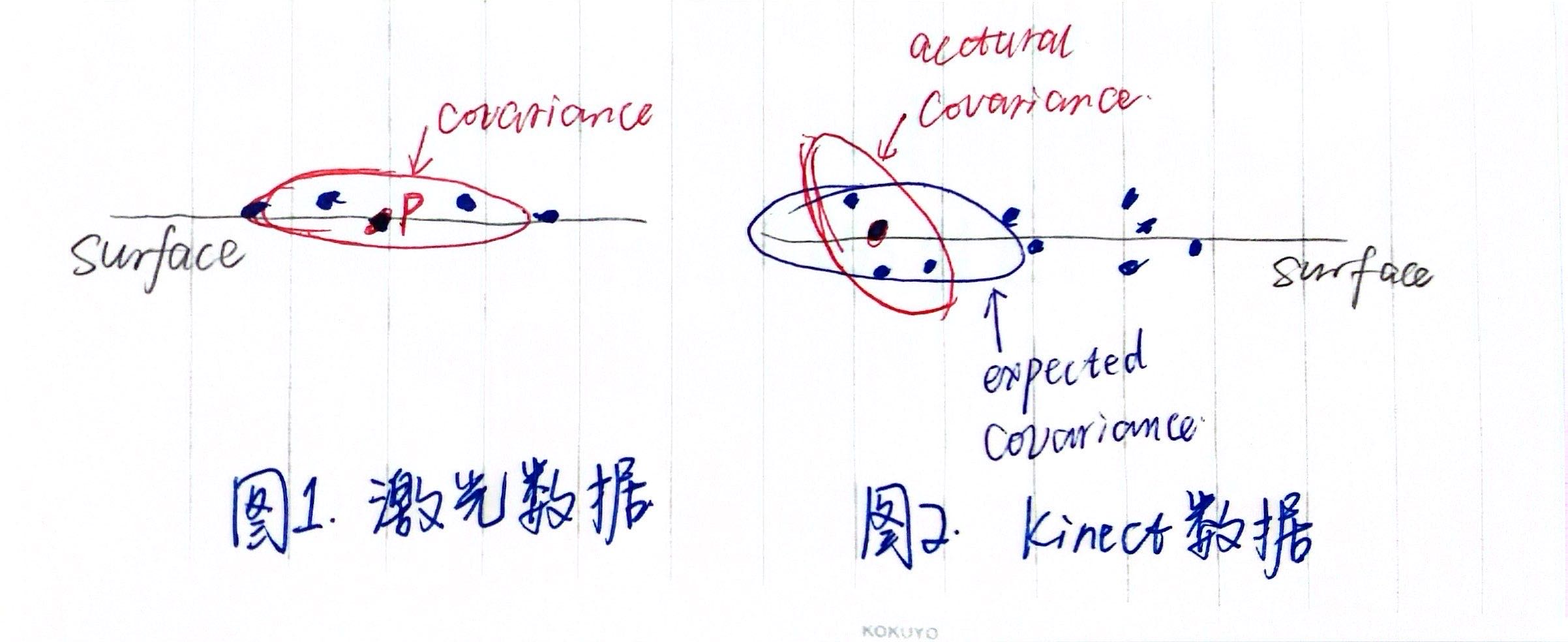
如上图所示，红色椭圆表示用实际点云拟合得到的协方差矩阵，在GICP算法中，期待其在surface方向上的特征值较大，而在法向量方向上的特征值较小，这样在匹配的时候就可以极大程度考虑到点云中的表面（surface）信息。但在Kinect中，由于原始数据的误差较大，很有可能导致协方差矩阵无法像在激光数据中那样好的表征与表面相关的信息（如图2），这样一来，加上这样的信息反而会干扰匹配的结果。

在此基础上我又对我之前提出的那个方法进行了进一步的分析。

与GICP类似的是，我也对点坐标做了数据分布上的假设，而且同样也是以正态分布为基础的。而与GICP针对单个点来进行正态分布拟合不同的是，我是先对点云进行粗略的网格划分，针对每个网格中的点来拟合正态分布，再根据网格中正态分布的方差 来分割网格中的点，并对分割出的每个部分再进行正态分布的拟合，直到最终分割的结果满足一定的条件而终止分割过程（这里的终止条件有待论证！）。分割过程终止后即可得到所谓叶子节点，相当于每一个叶子节点都代表着一个正态分布，在当前的实验中我是用其分布的均值来表示降采样后的点坐标。

而优化的过程与GICP基本一致，也是基于对应点来计算马氏距离（原有的思路）。只不过这里的点已不是GICP中所用的原数据点，而是经过处理后的。我认为理论上来讲处理后的数据点（或者说分布）应该能更好地表征原来点云的结构和分布信息（这一点同样有待论证）。

但是之前实验中出现的问题，说明分割后叶子节点的协方差信息同样不能很好地来表征原点云的结构信息，所以我猜测在这个用分割来细化分布的过程中，同样存在GICP中存在的问题（就是上面图片中的问题）。

另外经过上述比较我发现，我当前所提出的方法在匹配的过程上，与GICP的思想其实是一致的，不同的是对原始点云数据进行概率建模的过程（基于单个点的局部邻域拟合v.s.基于点集分割的拟合）。

当前方法与NDT算法比较³

由于涉及到正态分布的问题，我又重新看了一下NDT算法的文献。

在NDT算法，包括后面基于概率的匹配方法中，也是先对空间进行网格化（二维），再针对每个网格内的点来拟合正态分布，其结果就直接是一个二维的分布曲线，没有了点的概念，自然也就没有点与点的对应关系。其优化目标一般都是针对整个扫描帧的分布的最大后验概率。

这与GICP不同，GICP是以数据点为基础，对点分布的概率进行建模，而NDT则是直接用分布函数来替代了原始数据点。这样自然优化的目标函数也就有所区别。

而对于我当前提出的方法而言，虽然也是以点为基础来进行的，但是在对点的分布情况进行拟合时，是从整个点集出发，也可以说是以空间为单位来进行的。

总结与分析

基于以上讨论，我认为当前方法大体可以分为两个环节：针对原始点云的概率建模（即原来所说的非均匀下采样），以及建模结果在匹配过程中的应用。下面分别进行讨论。

• 建模

这一步的主要目的应该是使建模后数据点的概率模型最好的反映出原始点云的结构信息和分布信息。也就是说，这一步所达到的两个效果，一是针对点云结构的降采样（就是最初想要实现的目的），二是从概率意义上对结构信息的表征。

针对Kinect传感器，还应额外考虑其数据特点。现在为止的实验中，是通过用其深度值对分割阈值加权来将其考虑在内，但我觉得这个方法太过粗糙，没有充分利用其数据特点。关于这一点我现在还没有什么太好的想法。

• 匹配

现在我所用的匹配方法就是像ICP中一样，在每一步迭代中做点对点的对应，但这个点是经过我的方法降采样后的点，不再是原始的数据点。优化目标与GICP一样也是最小化对应点平均马氏距离。

关于这一点我也想过是否可以像在NDT中一样，尝试做分布之间的对应而避开点与点的对应，但经过一番考虑我觉得不太可行。一是在GICP的论文中就提到过，之所以采用欧式距离来进行对应点的计算而不是直接用分布来进行匹配是因为考虑到实时性，二是如果我这里避开了点的对应，那之前建模的过程中对点云实现的非均匀降采样就没有意义了。