Kinect深度误差分析
Published:
research journal, 2015.10.
前期工作
区别性降采样
通过控制采样频率来加强点云细节的描述
先进行网格划分,然后在网格内进行区别性的细分过程
点云的概率建模
在降采样的过程中,对每一个采样点进行概率建模,描述其分布情况
具体是用获得每个采样点的分割子集来拟合采样点的协方差,并将其应用于匹配过程,在尽量降低运算量的同时提高匹配精度
但Kinect原始数据点误差较大,且用来拟合每一个采样点的数据点不能太多(因为匹配时需要做point-to-point的对应,如果采样频率太低会有问题),导致拟合效果不佳,甚至会干扰匹配结果
Kinect深度数据误差分析
Kinect数据误差的三个方面
深度随机误差 random error
\[\sigma_Z=\frac{m}{fb}Z^2\sigma_{d'}\]深度分辨率 depth resolution
\[\Delta_Z=\frac{m}{fb}Z^2\]- 由disparity image量化引起
- 导致深度值不连续(即点云分层)的现象(见下一页图)
XY平面点密度 point density
\[\Delta_X=\Delta_Y=\frac{Z_K}{f}p_x\]- 指的是在空间XY平面(即平行于图像平面)的密度
- 用相邻两个pixel在空间XY平面上的间隔来表征
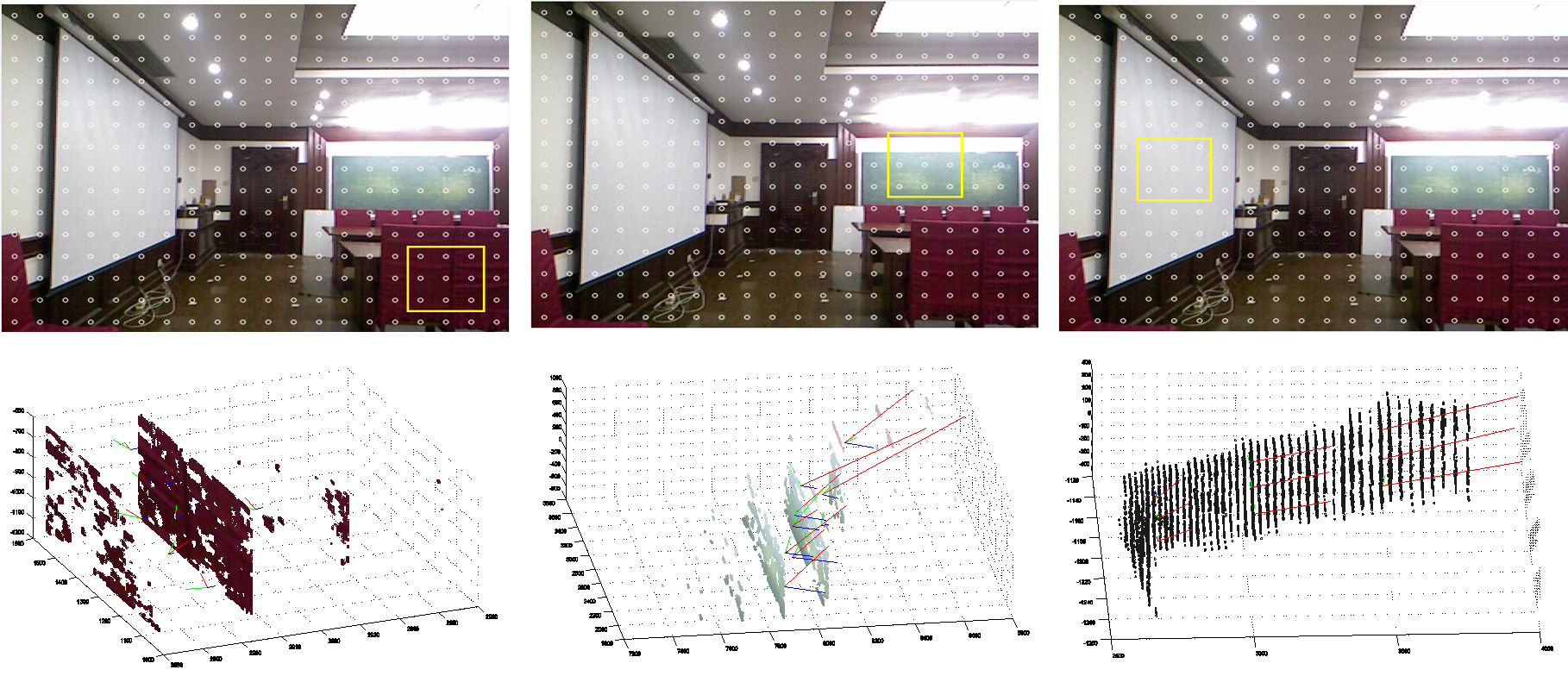
实验验证深度分辨率和XY平面密度与深度值之间的关系
- 真实环境中的同一平面(大致平行于图像平面)
- 距Kinect距离由近到远(大概1000mm~6000mm)

实验结果
对应上面9个图中的黄色矩形
| 深度(mm) | 分辨率(mm) | 密度(mm) |
|---|---|---|
| 1765 | 8 | 3.3 |
| 2150 | 14 | 4.0 |
| 2670 | 20 | 5.0 |
| 3200 | 30 | 6.3 |
| 3730 | 40 | 7.1 |
| 4210 | 52 | 8.3 |
| 4630 | 62 | 9.1 |
| 5230 | 80 | 10.0 |
| 5800 | 97 | 11.1 |
散点表示实测结果,实线表示理论结果(由图中公式得到)。
其中(标定得到)
\[\frac{m}{fb}=2.85e-5\] \[f=5.453mm\] \[p_x=p_y=9.3\mu m\]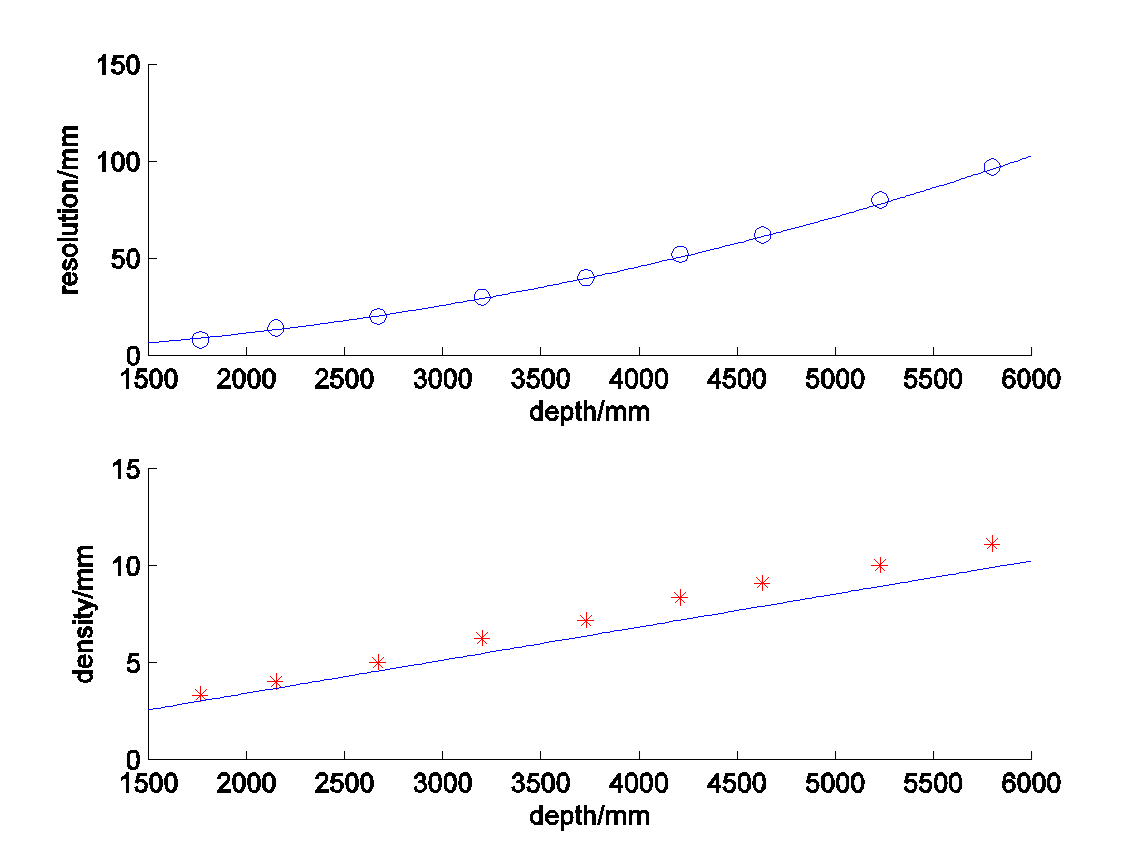
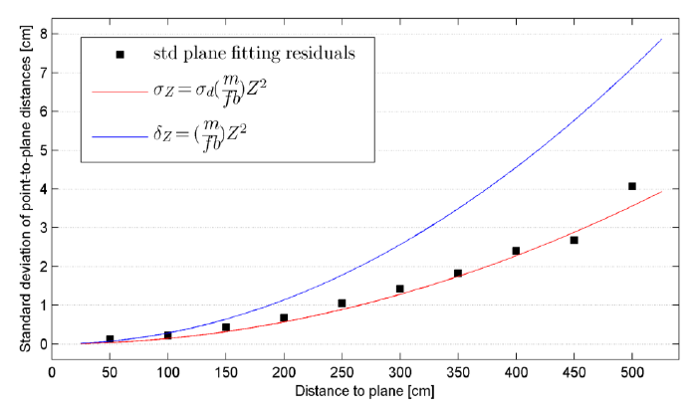
引用他人验证随机误差与深度之间关系的实验结果1:
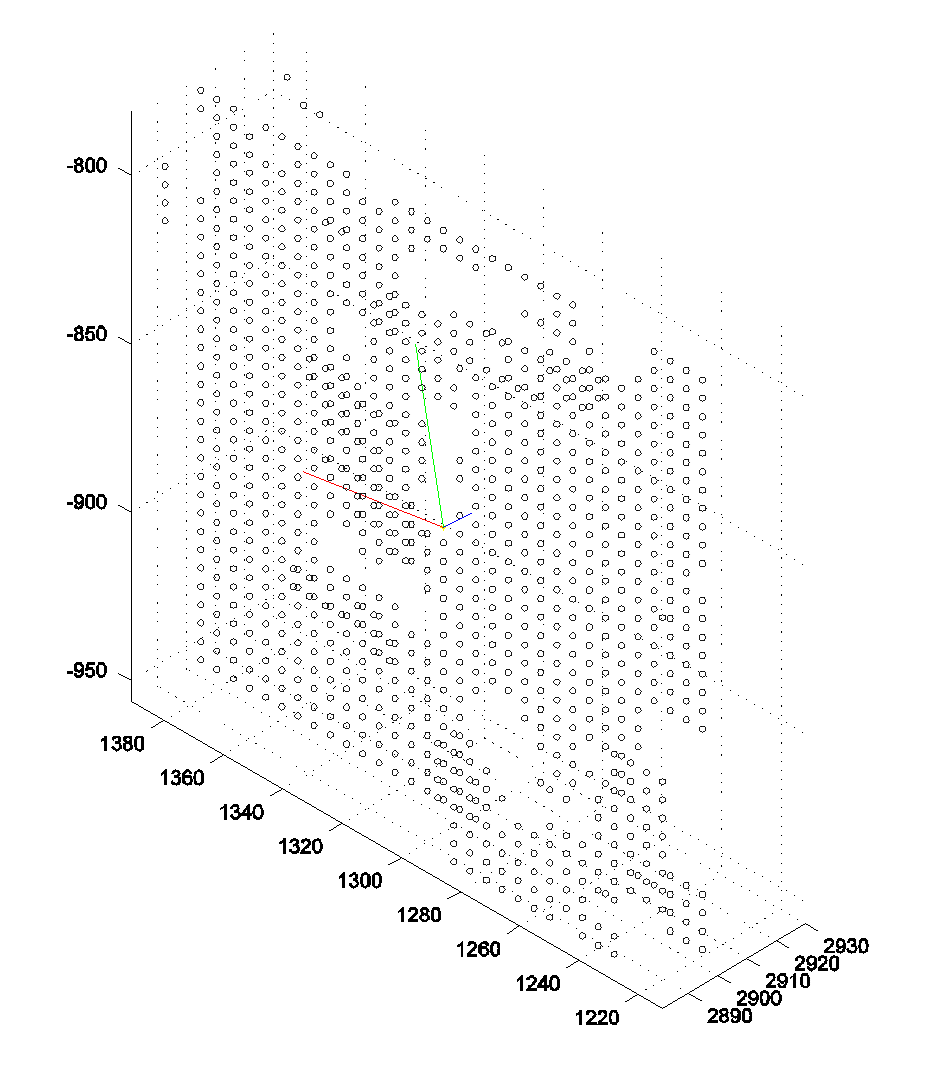
距Kinect不同深度的平面,平面大致垂直于光轴,4500个采样点,拟合平面,计算残差。
图中散点是实验结果,红线是随机误差理论值,蓝线是分辨率理论值。
实验结果分析
在深度值6000mm以内:
深度的随机误差在50mm以内,并随深度平方增长
深度分辨率在100mm以内,并随深度平方增长
XY平面点密度10mm以内,并随深度线性增长
文献1中说当拟合点数足够大时即可以忽略分辨率的影响(图中蓝色曲线),但文中并未展示相关实验结果来验证这一点(不过文中实验用到4500个数据点来做拟合确实已经足够多)。
也就是说,在拟合数据点并不是足够多的时候(细化分割的时候很容易产生这样的情况),还是需要考虑分辨率,甚至点密度的影响。
在我的实验中,粗分15\(\times\)20网格时,每个网格内的数据点1024个。
理论上,XY方向上的随机误差小于等于Z方向随机误差的一半。
\[\sigma_X=\frac{mx}{f^2b}Z^2\sigma_{d'}\le\frac{1}{2}\sigma_Z\]最终目标是计算出的协方差尽量拟合局部平面。局部平面在一定程度上即可表征点云结构信息,但协方差的计算受到点坐标不确定度的影响,并且,点坐标不确定度与深度之间存在一定的定量关系,想要利用此定量关系来校正协方差的计算过程。
协方差校正
考虑两种情况
若局部平面平行于图像平面,须保证局部平面的大小远大于深度分辨率以及深度随机误差;
若局部平面垂直于图像平面,须保证局部平面的大小远大于XY平面上点的密度以及XY方向上的随机误差;
即所拟合局部平面的大小,须要足够大,以至于可以忽略当前深度值下平面法向量方向的不确定度。

下面需要考虑:如何表征拟合局部平面的大小。
首先确定用来拟合局部平面的点在空间上是否邻近,即在Z方向上是否邻近,因为是在图像平面上划分网格,所以XY方向上一定是邻近的。若不是邻近,说明取自不同的表面,则进行分割(即之前所做的二叉树分割)。
若已确定在空间上是邻近的,则可以用协方差来表征其分布,若某一个方向上的特征值相较于其他两个方向来说足够小,则可以表征局部平面。若已经确定是平面,判断较大的两个特征值与当前深度下较小特征值对应特征向量方向上(即法向量方法)点坐标不确定度之间的关系。
如何确定某个方向上的不确定度?(这个还没有成熟的想法,我后面再深入考虑一下)。
关于分割
由于网格划分是在图像平面上进行的,所以投影上三维空间中的坐标在XY方面上一定是邻近的,所以在分割时应该只需要考虑Z方向(即深度值)。直观上也可以看到,比较大的特征值都在Z方向。

实验一:
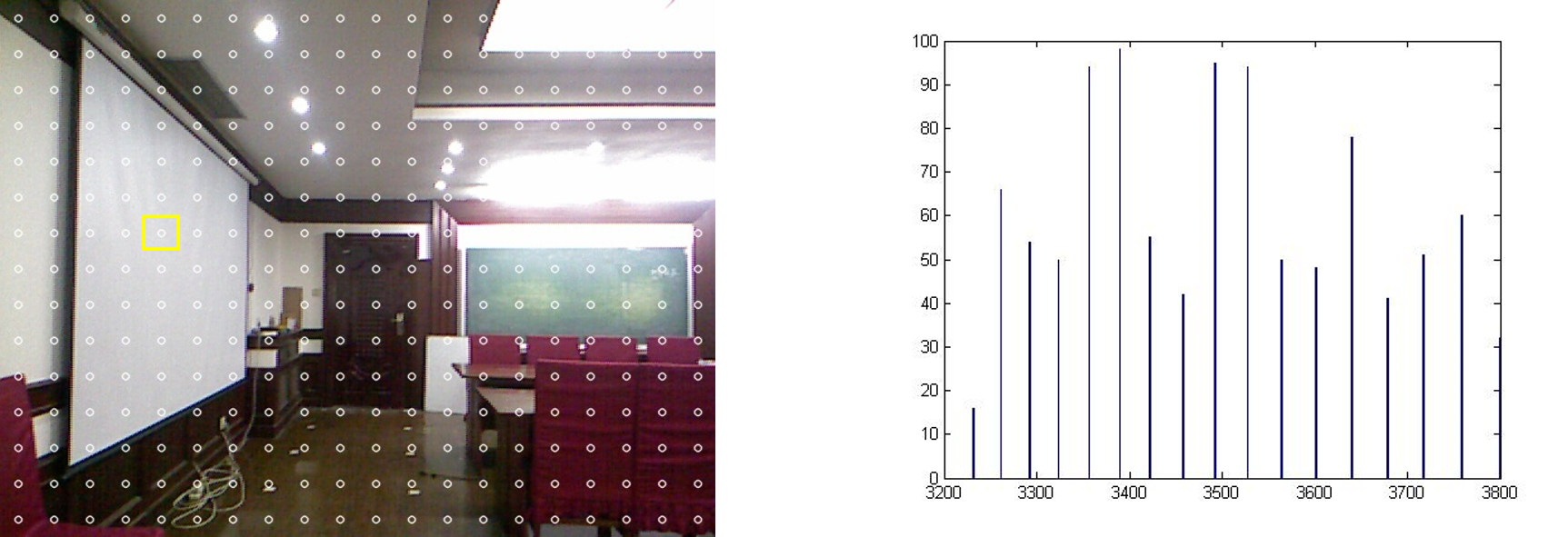
取自同一表面(大致平行于图像平面),计算某一区域内(黄色矩形)深度值的直方图。
横坐标为深度值,纵坐标为该深度值的采样点数(disparity value的量化导致深度值也是离散的)。
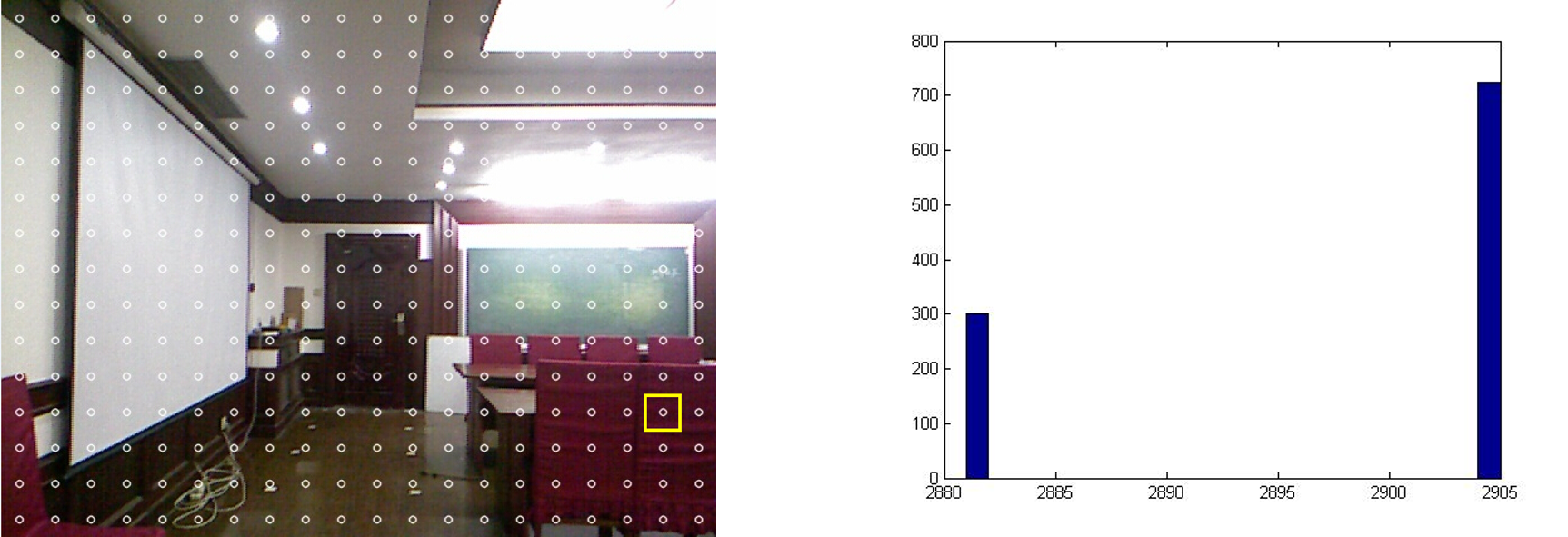
实验二:
取自同一表面(与图像平面呈一定角度)。
实验三:
取自不同表面(大致平行于图像平面)。
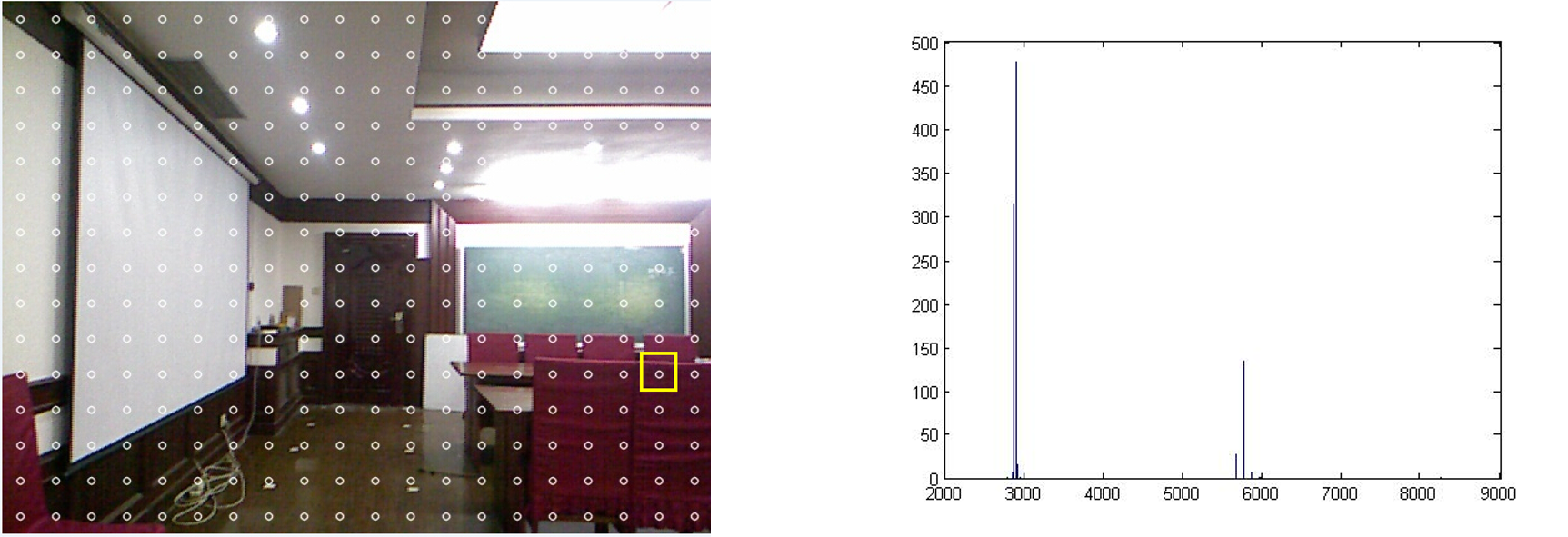
由以上实验可以看出,若某一区域内的点取自不同表面,可以很明显看出其深度值分布呈现两个(或多个)峰值,且间隔较远(如实验三);若取自平行于图像平面的同一表面,则其深度值集中于某一深度值附近(如实验一);若取自与图像平面呈一定角度的表面,则其深度值随机(一般较均匀)地分布于某一区间内(如实验二)。
因此,在对每一个网格内的点进一步进行分割时,只需要考察其深度值的分布情况即可,但分割阈值的设置仍须考虑其不确定度随深度值的变化情况。
关于某个方向上的不确定度
只考虑随机误差,已知XYZ三个方向上的方差分别是\(\sigma_X, \sigma_Y, \sigma_Z\),其中\(\sigma_X=\sigma_Y\le\frac{1}{2}\sigma_Z\)。假设\(\sigma_X, \sigma_Y, \sigma_Z\)分别为椭球体的三个轴,构成一个长轴沿Z方向的椭球体,方程为
\[\frac{(x-p_x)^2}{\sigma_x^2}+ \frac{(y-p_y)^2}{\sigma_y^2}+ \frac{(z-p_z)^2}{\sigma_z^2}=1\]
协方差矩阵特征值 v.s. 点云误差与分辨率
首先对特征值与点云误差及分辨率的可比性进行考察。
如果从主成分分析的角度来看,协方差矩阵的特征向量组成一组正交基,若将点云投影到以特征向量为基的空间中,而此时点云在这个空间的协方差矩阵为对角阵,对角线元素为特征值,所以特征值可以表示点云在这个空间中各个维度上的方差。
而点云误差是以标准差的形式表示的,而如果我可以计算出在任意方向上的误差值,自然也可以得到特征向量方向的误差值,所以可以将特征值开方,转化为标准差,二者即具有可比性。
想要通过实验寻找随深度增加,协方差矩阵拟合情况与数据误差之间的关系。先通过从一个场景中选取几个位置进行拟合,从中发现一些规律。以下所有实验中,每次拟合所用点数相同(1000个点),并且均已将特征值进行开方。

| 位置 | 平面大致姿态 | 深度(mm) | 特征值开方(mm) | 理论深度分辨率(mm) | 理论XY方向点密度(mm) |
|---|---|---|---|---|---|
| 124 | 与图像平面呈角度 | 3500 | 157.4884 60.5908 7.9262 | 34 | 6 |
| 176 | 平行于图像平面 | 8000 | 158.6212 143.2540 86.5504 | 182 | 14 |
| 257 | 平行于图像平面 | 2900 | 51.6501 50.1185 9.5669 | 24 | 5 |
位置124
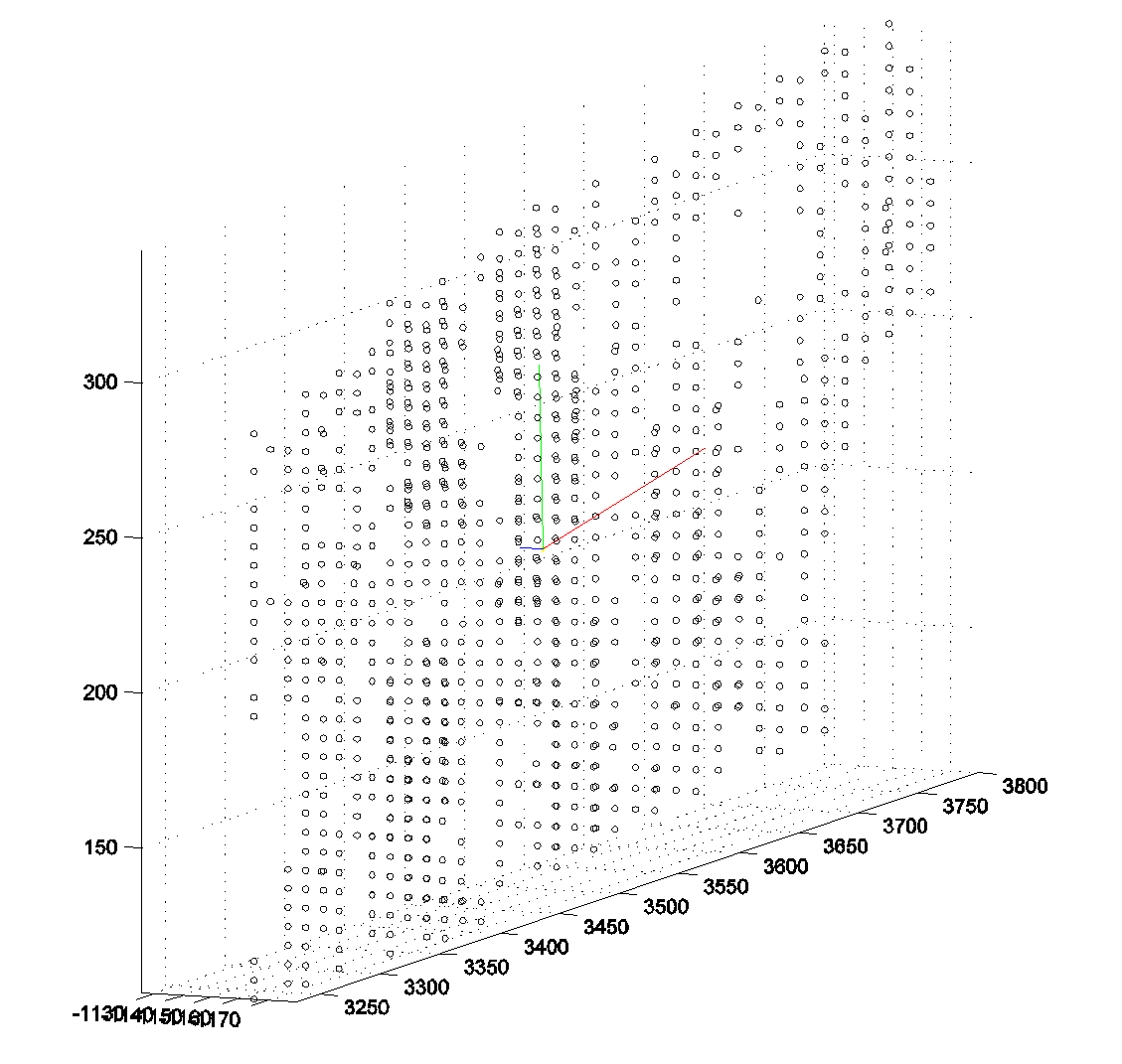
位置176
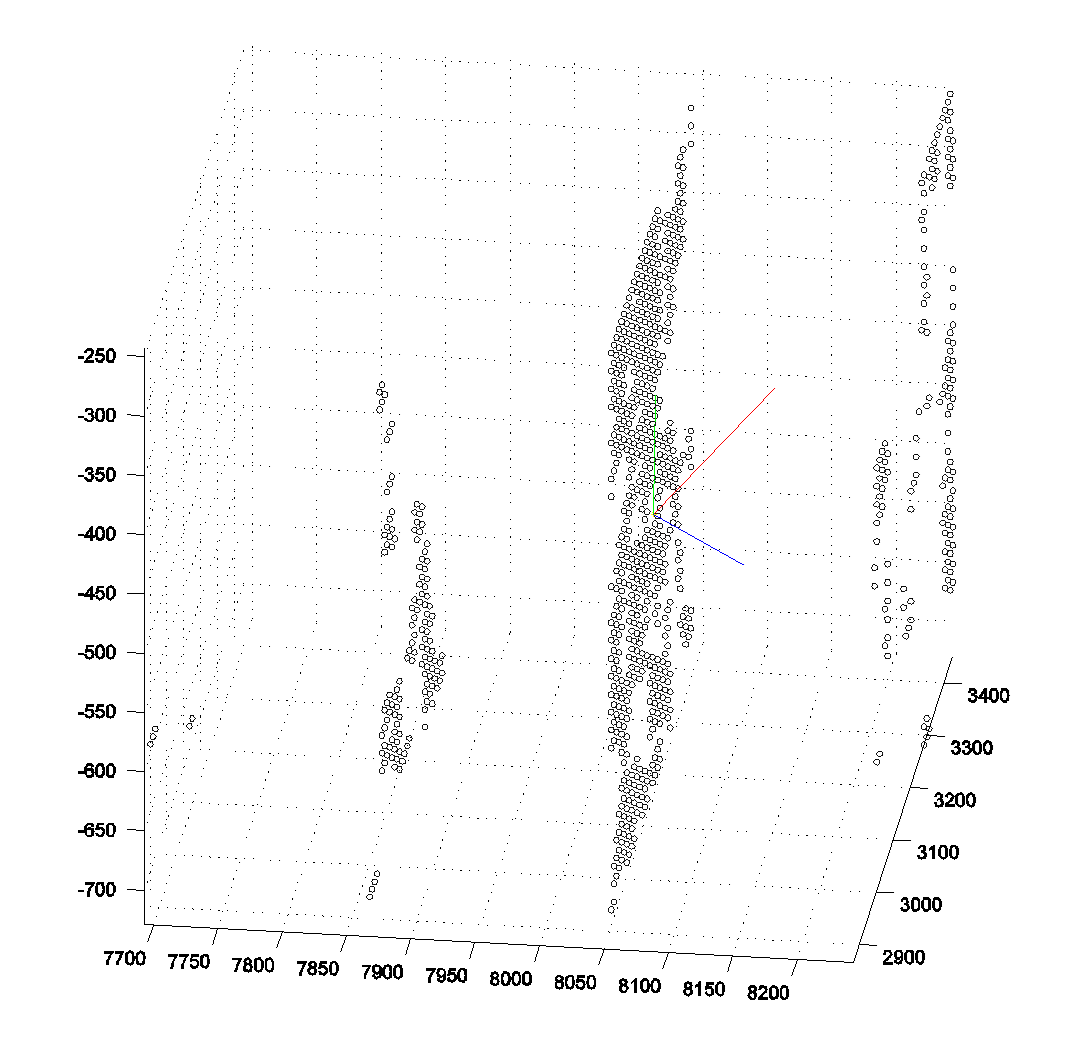
位置257
结果分析: 首先可以看出,对于相同数量的点,随深度增加,其协方差矩阵的特征值是增大的,因为随着深度增加,单位空间内所包含点的数量在减少,也即每个点所占据的空间在增加,再加上随机误差随深度增加的规律,导致其特征值增幅明显。
下面仍是针对同一姿态的平面来进行分析,还是之前实验中的9个场景,选取平行于图像平面的平面来进行实验,是因为深度值方向上的不确定度要远远大于XY方向上,所以平行于图像平面的平面在拟合时应该是最困难的。

| Depth/mm | sqrt(eigenvalue)/mm | Sigma(z)/mm | Sigma(x)/mm | Sigma(y)/mm | Deta(z)/mm | Deta(xy)/mm |
|---|---|---|---|---|---|---|
| 1760 | 32.7351 30.3337 4.2962 | 4.4227 | 0.3621 | 0.4827 | 8.8453 | 3.0046 |
| 2150 | 38.8531 37.1680 9.0576 | 6.6212 | 0.5420 | 0.3614 | 13.2425 | 3.6763 |
| 2650 | 48.5685 45.8462 11.8248 | 10.0607 | 0.8236 | 0.5491 | 20.1214 | 4.5316 |
| 3240 | 58.0035 55.9757 17.2835 | 15.0261 | 1.2301 | 0.8201 | 30.0522 | 5.5381 |
| 3730 | 68.2145 63.9269 34.9284 | 19.8492 | 2.7082 | 1.0833 | 39.6983 | 6.3652 |
| 4210 | 74.1820 72.3753 43.1314 | 25.2997 | 3.4519 | 1.3807 | 50.5994 | 7.1862 |
| 4680 | 82.7222 81.1108 52.5952 | 31.3268 | 4.2742 | 1.7097 | 62.6536 | 7.9965 |
| 5230 | 100.8529 89.9577 52.0296 | 39.0334 | 5.3257 | 2.1303 | 78.0667 | 8.9260 |
| 5830 | 128.0633 99.8587 83.5054 | 48.4463 | 6.6099 | 2.6440 | 96.8926 | 9.9442 |
结果分析: 三个方向特征值均随深度增加而增加,且与误差值呈现某种正相关的关系,随深度增加,三个方向上的特征值的差异也在明显减小。实验中所取点数较多,可以想象若点数变少,到了一定的深度值的时候三个方向上的特征值会趋于一致(这应该就是导致之前实验中加上法向量信息后匹配结果不好的原因)。
以上只是一些定性的分析,更具体分析以及如何应用到方法中的工作我后面会继续进行。